Question

An aeroplane at a height of 600m passes vertically above another aeroplane at an instant where their angles of elevation at the same observing point are ${60^ \circ }$and ${45^ \circ }$ respectively. How many metres higher is the one from the other?
A. $286.53$
B. $274.53$
C. $253.58$
D. $263.83$

Answer 1

To solve the given question first draw the diagram to take a rough idea to solve the problem. Here in this question, it is given that an aeroplane is 600 m high when it passes vertically above another aeroplane at that instant. The angle of elevation of both the planes is also given to us. We have to find the distance between both the planes.
We have to find the distance of another plane with the ground. By applying trigonometric ratios formula, we will find the distance of another plane with respect to the ground. After that take the difference of distance of first plane ad another plane with respect to ground respectively, to find the required solution.

Complete step by step answer:

First of all, draw the diagram according to the given statement and the diagram is given below:

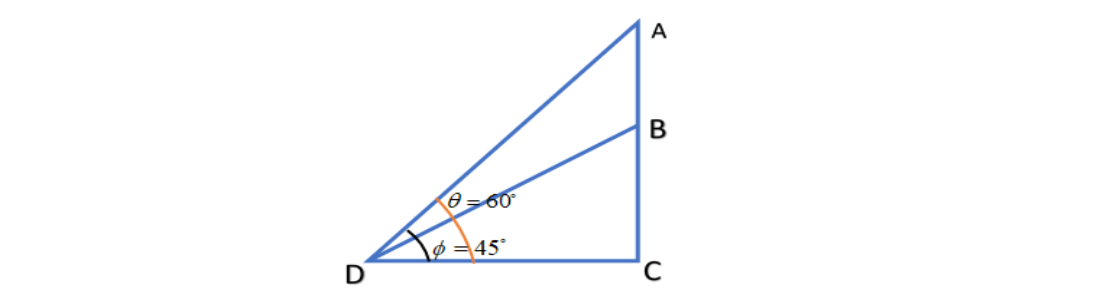
Let suppose AC be the distance between the first aeroplane and ground. Let suppose BC be the distance between second and ground.
Here, we have drawn the diagram and we have to find AB while we know the value of BC and both the angles.
To find the value of DC as follows:
In $\vartriangle ACD$, Here you can see the angle made by DC and DA is 60 degree and DC and AC are base and perpendicular respectively then
$\Rightarrow \tan \theta = \dfrac{{AC}}{{DC}}$
Put the value of AC i.e. 600m we get,
$\Rightarrow \tan {60^ \circ } = \dfrac{{600}}{{DC}}$
$\Rightarrow \sqrt 3 = \dfrac{{600}}{{DC}}$
$\Rightarrow DC = \dfrac{{600}}{{\sqrt 3 }}$
Multiply numerator and denominator by $\sqrt 3$we get,
$\Rightarrow DC = \dfrac{{600 \times \sqrt 3 }}{{\sqrt 3 \times \sqrt 3 }}$
$\Rightarrow DC = \dfrac{{600 \times \sqrt 3 }}{3}$
Divide 600 by 3 we get,
$\Rightarrow DC = 200\sqrt 3 m$…..(1)
Now, you know the value of DC and you can find the value of BC as follows:
In $\vartriangle BCD$, here you can see that angle made by aeroplane is 45 degree and DC and BC are base and perpendicular respectively then
$\Rightarrow \tan {45^ \circ } = \dfrac{{BC}}{{DC}}$
$\Rightarrow 1 = \dfrac{{BC}}{{DC}}$
$\Rightarrow BC = DC = 200\sqrt 3 m$……..(2)
To find the value of AB subtract BC from AC. By putting the values of AC and BC from equation 1 and 2 respectively we get,
$\Rightarrow AB = AC - BC = 600 - 200\sqrt 3 m$
Taking 200 common from both terms we get,
$\Rightarrow 600 - 200\sqrt 3 = 200(3 - \sqrt 3 )m$
Putting the value of $\sqrt 3$in the above i.e. $\sqrt 3 = 1.7321$we get,
$\Rightarrow AB = 200(3 - 1.7321) = 200 \times 1.2679m$
$\Rightarrow AB = 253.58m$
Hence, option c is the correct answer.

Note: Here the common mistake done while solving is the students can get confused and take BC as 600m but they had said the first aeroplane is above the second plane. So, take care of this thing. Second, in the given options the numbers are in decimals up to 2 decimals place so take the value of square root 3 up to 4 decimals place to get the correct answer.