Question

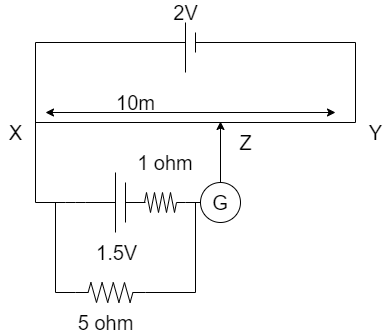
An accumulator of emf 2V and negligible internal resistance is connected across a uniform wire of length $10m$ and resistance $30\Omega$. The appropriate terminals of a cell of emf $1.5V$ and internal resistance $1\Omega$ is connected to one end of the wire, and the other end of the cell is connected through a sensitive galvanometer to a slider on the wire. If the balancing changes when the cell of $1.5V$ is shunted with a resistance of $5\Omega$ is $\dfrac{x}{4}m$. Find $x$.

Answer 1

Resistance is defined as the opposition offered to the flow of electrons in a current carrying conductor. Also the e.m.f. is the energy provided by a cell to the charge passing through it. When the electric potential decreases along the path following in a circuit, then there is voltage drop.

Complete step by step answer:
Step I:
Given that the cell is connected to a galvanometer, there will be a deflection when the galvanometer is made to slide on the wire.
Let the length of the wire XY is $= x$ such that the current $I$ flowing through that part of the wire is zero and the galvanometer shows a zero deflection. That is
${I_g} = 0$
Also voltage drop on the balancing length is given in accordance to Ohm’s Law,
$V = IR$
Here $\rho$ is the resistance
So, $V = I\rho x$

Step II:
When there is no current in the wire and galvanometer shows zero deflection, then
Voltage across the circuit = Voltage across the part of wire XZ
Let $\rho$ be the resistance of the wire.
Since only two resistances are in parallel along the part of the wire XZ. The equivalent resistance in a parallel circuit is the reciprocal of the sum of individual resistances and is given by
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
On substituting the corresponding values,
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = (\dfrac{1}{1} + \dfrac{1}{5})$
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{6}{5}$
Step III:
Also the resultant e.m.f is given by
${E_{eq}} = \dfrac{{\dfrac{{{E_1}}}{{{r_1}}} + \dfrac{{{E_2}}}{{{r_2}}}}}{{\dfrac{1}{{{R_{eq}}}}}}$
Substituting the values and solving,
$\Rightarrow {E_{eq}} = \dfrac{{\dfrac{{1.5}}{1} + \dfrac{0}{5}}}{{\dfrac{6}{5}}}$
On simplifications,
$\Rightarrow {E_{eq}} = \dfrac{5}{4}volt$
Step IV:
Let $y$ is the length of the wire that is to be calculated when slider is moved and when the galvanometer shows zero deflection,
$\Rightarrow \dfrac{5}{4} = \dfrac{2}{3} \times \dfrac{{30}}{{10}} \times y$
On simplification,
$\Rightarrow y = \dfrac{{25}}{4}m$
On further simplification,
$\Rightarrow x = 25m$

The length of $x$ is $25m$.

Note:
It is important to note that the terms e.m.f and voltage are different. When external forces work to move a charge from one point to another then the voltage produced is represented by e.m.f. But the voltage denotes the potential difference across two points.