Solveeit Logo
Login

Question

Question: An AC voltmeter in an L-C-R circuit reads 30 volts across resistance, 80 volts across inductance and...

An AC voltmeter in an L-C-R circuit reads 30 volts across resistance, 80 volts across inductance and 40 volts across capacitance. The value of the applied voltage will be
A. 50 Volt
B. 25 Volt
C. 150 Volt
D. 70 Volt

Explanation

Solution

The question is a direct one. The value of the combination voltage will be the value of the applied voltage. The combination voltage is calculated as the root of the sum of the square of voltage value across the resistor and the square of the difference of the voltage value across the capacitor and voltage value across the inductor.

Formula used:
VC=VR2+(VC−VL)2{{V}_{C}}=\sqrt{V_{R}^{2}+{{({{V}_{C}}-{{V}_{L}})}^{2}}}

Complete step by step answer:
A diagram representing a circuit diagram of L-C-R

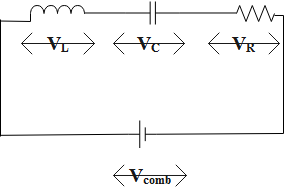
The formula used to find the value of the voltage applied, that is, the value of the combined voltage is given as follows:

VC=VR2+(VC−VL)2{{V}_{C}}=\sqrt{V_{R}^{2}+{{({{V}_{C}}-{{V}_{L}})}^{2}}}

Where VR{{V}_{R}}is the voltage value across the resistor, VC{{V}_{C}} is the voltage value across the capacitor and VL{{V}_{L}} is the voltage value across the inductor.

From the data, we have,
The voltage value across the resistor is, VR=30 V{{V}_{R}}=30\,V
The voltage value across the capacitor is, VC=40 V{{V}_{C}}=40\,V
The voltage value across the inductor is, VL=80 V{{V}_{L}}=80\,V
Even though the value of the voltage across the capacitor is less than that across the inductor, as we square the difference, so, there won’t be a change in the value.
Therefore, the voltage applied is calculated as follows.

& {{V}_{C}}=\sqrt{{{30}^{2}}+{{(40-80)}^{2}}} \\\ & \Rightarrow {{V}_{C}}=\sqrt{900+1600} \\\ \end{aligned}$$ Continue further calculation. $$\begin{aligned} & {{V}_{C}}=\sqrt{2500} \\\ & \therefore {{V}_{C}}=50\,V \\\ \end{aligned}$$ **As the value of the applied voltage in an L-C-R circuit is obtained to be equal to 50 V, thus, the option (A) is correct.** **Note:** The formula for finding the value of the combination voltage should be known to solve such problems. Even by providing the values of the combination voltage itself along with the values of the two of the three voltage values, the other voltage value can be asked. The units of the parameters should be taken care of.