Question
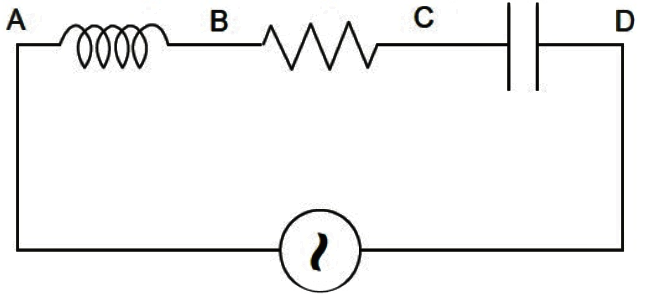
Question: An AC voltmeter connected between points A and B in the circuit below reads 36V. If it is connected ...
An AC voltmeter connected between points A and B in the circuit below reads 36V. If it is connected between A and C, the reading is 39V. The reading when it is connected between B and D is 25V. What will the voltmeter read when it is connected between A and D? (Assume that the voltmeter reads true rms voltage values and that the source generated a pure AC.)
(A)481V(B)31V(C)61V(D)3361V
Solution
The net rms potential across A and D will be due to the root sum of squares of, voltage drop across the resistance and the difference in the voltage drop between the inductor and capacitor. This difference in potential is because when connected in series, the inductor and capacitor are always out of phase with respect to each other.
Complete answer:
Let us first assign some terms that we are going to use later in our solution. Let the voltage drop across the resistance be given by VR, the voltage drop across the capacitance by VC and finally, the voltage drop across the inductor be VL .
Then, according to the question, we have:
⇒(VL)2=362
And,
⇒VL2+VR2=392
Then, using the above equation, we can calculate the voltage drop across the resistance as:
⇒VR2=392−362∴VR=15V
It has also been given in the problem that:
⇒VL2+VC2=252⇒VC2=252−152∴VC=20V
Now that, we have the potential drop across each component of the circuit, thus we can calculate the potential drop across all of them as:
⇒VAD=(VR2)+∣VL−VC∣2
Putting the values of all the terms in the right-hand side of the equation, we get:
⇒VAD=152+(36−20)2⇒VAD=225+256∴VAD=481V
Hence, the voltage drop or the reading in the voltmeter when it is connected cross AD will be 481V.
Hence, option (A) is the correct option.
Note:
A capacitor and inductor are always out of phase, that is, they have a phase difference of 1800 when connected in series, and the phase difference of resistor lies in between them. This is the reason why in our final equation we wrote the square of voltage of the resistor term separately from the other two.
