Question

An AC source generating a voltage $V = {V_m}\sin (\omega t)$ is connected to a capacitor of capacitance C. Find the expression of the current i flowing through it. Plot a graph of V and i versus $\omega t$ to show that the current is π/2 ahead of the voltage.

Answer 1

Understand the concept of current as flow rate of charge per unit time. Also use the formula for voltage passing through a capacitor of capacitance C to deduce the expression. Draw the plot for different values of $\omega$.

Complete answer:
We know that there is an AC source generating a voltage of $V = {V_m}\sin (\omega t)$, that is attached to a capacitor of capacitance C.
Now, we know that the voltage passing through the capacitor V is equal to $V = Q/C$, where Q is the charge value in coulombs and C is capacitance value in farads.
Now, current I in any circuit is defined as the flow rate of charges per unit time. Mathematically,
$i = \dfrac{{dQ}}{{dt}}$
Now, rearranging the Voltage inside a capacitor equation we get,
$V \times C = Q$
Substituting this in the current equation we get,
$i = \dfrac{{d[V \times C]}}{{dt}}$
Now, V is given as ${V_m}\sin (\omega t)$for the given circuit, substituting that in the above equation we get$i = \dfrac{{d[C \times {V_m}\sin (\omega t)]}}{{dt}}$
Applying differentiation inside, we get,
$i = C \times \dfrac{{d[{V_m}]}}{{dt}} \times \omega \cos (\omega t)$
Note: Differentiation of $\sin (\omega t)$is $\cos (\omega t)$multiplied by differentiation of $\omega t$, which is $\omega$.
Now, $\cos (\omega t)$can also be written as $\sin (\omega t + \pi /2)$, due to quadrants.
$i = C \times \dfrac{{d[{V_m}]}}{{dt}} \times \omega \times \sin (\omega t + \pi /2)$
Taking constant term C and$\omega$to the denominator,
$i = \dfrac{{\dfrac{{d[{V_m}]}}{{dt}} \times \sin (\omega t + \pi /2)}}{{1/C \times \omega }}$
Now, we know that the instantaneous current passing through a capacitor of capacitance C is given as ,
${i_m} = C \times \dfrac{{d[{V_m}]}}{{dt}}$
Applying this concept to the above equation,
$\Rightarrow i = {i_m}\sin (\omega t + \pi /2)$
Where ${i_m} = \dfrac{{{V_m}}}{{1/C\omega }}$
The term $1/C\omega$ is called capacitive reactance and is represented as ${X_c}$.
Now, plot the graph for different values of $\omega t$ ranging from zero to${360^ \circ }$.
The resulting graph will see that the current is leading by a phase difference of $\pi /2$.

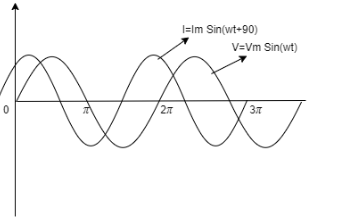
Thus the expression is derived and the graph is drawn accordingly.

Note:
Capacitive reactance is defined as the total opposition to the current flow offered by a capacitor of capacitance C. It is similar to resistance but it’s not equal to resistance. It is represented by the term${X_c}$.