Question

An AC circuit contains a variable inductor $L$, connected in series with a light bulb of resistance $R$ as shown. Assume that the resistance of the light bulb is independent of its temperature. Now it is desired to reduce the power of the light bulb to one fourth then (frequency of ac source is $\dfrac{R}{{2\pi {L_o}}}$ where ${L_o}$​ is in initial inductance).
This question has multiple correct options.

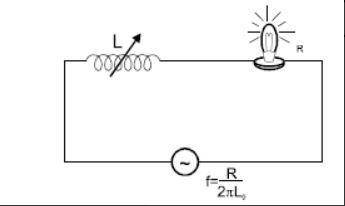
(A) power factor of the circuit should be reduced to half.
(B) inductance of the circuit should be increased by the factor of $\sqrt 3$.
(C) impedance of the circuit should be increased by the factor of $4$.
(D) R.M.S. current in the circuit should be reduced to half.

Answer 1

The above given problem can be solved using the formula that is derived from the formulas of power of in a circuit. With respect to variable inductance of the A.C. circuit and resistance of the light bulb with an initial inductance of ${L_o}$.

Formulae Used:
The power of the light bulb is;
$P = \dfrac{{V_R^2}}{R}$
Where, $P$ denotes the power of the bulb, ${V_R}$ is the voltage across the resistor, $R$ the resistance of the resistor.

Complete step-by-step solution:
The data given in the problem is;
Inductor of the ac circuit of inductance, $L$.
Resistor of resistance, $R$.
Frequency of the A.C. source is, $\dfrac{R}{{2\pi {L_o}}}$.
The power of the light bulb is;
$P = \dfrac{{V_R^2}}{R}$
Where, ${V_R} = {V_S}\cos \emptyset$, $\cos \emptyset = \dfrac{R}{Z} = \dfrac{R}{{\sqrt {{R^2} + {\omega ^2}{L^2}} }}$;
Since $P\,\alpha \,\cos \emptyset \left( {\cos \emptyset = P.F.} \right)$
If power reduces to ${\dfrac{1}{4}^{th}}$then P.F. reduces to half.
since the $\cos \emptyset \,\alpha \,\dfrac{1}{Z}$
Let’s assume if P.F. reduces to half, then the impedance increases by a factor of $2$
by equating on both sides we get;
$2\sqrt {{R^2} + {\omega ^2}L_0^2} = \sqrt {{R^2} + {\omega ^2}L{'^2}} \\\ L' = \sqrt 7 {L_0} \\\$
Where $L'$ denotes the inductance of the ac circuit. ​
$P = i_{rms}^2R$
Where $i_{rms}^2$ denotes the current of the RMS.
Therefore, the RMS current reduces to half.
Therefore, the power factor of the circuit should be reduced to half and the R.M.S. current in the circuit should be reduced to half.

Hence, the option (A) power factor of the circuit should be reduced to half and the option (D) R.M.S. current in the circuit should be reduced to half is the correct answer.

Note:- If the reduction factor of the A.C circuit changes from the value of one forth, then the value obtained by it will get affected greatly, that is there will be change in the power factor and the R.M.S value of the A.C. source of the circuit.