Solveeit Logo
Login

Question

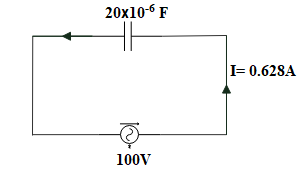
Question: An a.c. supply of 100 volts is applied to a capacitor of capacitance \(20\mu F\). If the current in ...

An a.c. supply of 100 volts is applied to a capacitor of capacitance 20μF20\mu F. If the current in the circuit is 0.628A0.628A, the frequency of a.c. must be
a) 50 Hz
b) 60 Hz
c) 25 Hz
d) 40 Hz

Explanation

Solution

The given circuit is a purely capacitive circuit. This means that only a capacitor is present in the circuit along with the alternating current source and no resistor or inductor is present. Therefore, only the capacitor is consuming energy and we must modify the formula of impedance accordingly. Impedance is the total resistance present against the current in the circuit.

Complete step-by-step solution:
Impedance of a LCR circuit is given as:
Z=R2+(XL−XC)2Z=\sqrt{{{R}^{2}}+{{\left( {{X}_{L}}-{{X}_{C}} \right)}^{2}}}
Where,
R=R= Resistance of the resistor present
XL={{X}_{L}}=Inductive reactance of the inductor present. It is further given as XL=ωL{{X}_{L}}=\omega L

ω=2πν\omega =2\pi \nu , ⇒XL=2πνL\Rightarrow {{X}_{L}}=2\pi \nu L
Where, ν=\nu =frequency of the alternating current provided to the circuit and L=L=inductance of inductor
XC={{X}_{C}}=Capacitive reactance of the capacitor present. It is further given as XC=1ωC{{X}_{C}}=\dfrac{1}{\omega C}
ω=2πν\omega =2\pi \nu , ⇒XC=12πνC\Rightarrow {{X}_{C}}=\dfrac{1}{2\pi \nu C} ………….. equation (1)
Where, ν=\nu =frequency of the alternating current provided to the circuit and C=C=capacitance of capacitor

Since, no resistor or inductor is present in the circuit,
Therefore,
Z=0+(0−XC)2 ⇒Z=XC \begin{aligned} & Z=\sqrt{0+{{\left( 0-{{X}_{C}} \right)}^{2}}} \\\ & \Rightarrow Z={{X}_{C}} \\\ \end{aligned}

Now,
The voltage,VVof the a.c. circuit is given as:
V=IZV=IZ
Here, I=I=current in circuit and Z=XCZ={{X}_{C}}
⇒XC=VI\Rightarrow {{X}_{C}}=\dfrac{V}{I}
From equation (1),
⇒12πνC=VI\Rightarrow \dfrac{1}{2\pi \nu C}=\dfrac{V}{I}

Given that voltage = 100 volts, current = 0.628A0.628Aand capacitance =20μF=20×10−6F20\mu F=20\times {{10}^{-6}}F
⇒12πν(20×10−6)=1000.628 ⇒ν=0.6282(3.14)(20×10−6)(100) ⇒ν=12×100 ⇒ν=50Hz \begin{aligned} & \Rightarrow \dfrac{1}{2\pi \nu \left( 20\times {{10}^{-6}} \right)}=\dfrac{100}{0.628} \\\ & \Rightarrow \nu =\dfrac{0.628}{2\left( 3.14 \right)\left( 20\times {{10}^{-6}} \right)\left( 100 \right)} \\\ & \Rightarrow \nu =\dfrac{1}{2}\times 100 \\\ & \Rightarrow \nu =50Hz \\\ \end{aligned}
The frequency of alternating current must be 50Hz.

Therefore, the correct option is (a) 50Hz.

Note:
An AC (alternating current) analysis is where we limit ourselves to inputs to our circuits that look like sinusoids, cosines or sines. The voltage and current are represented as sinusoidal waves and written in sinusoidal equations which make their study comparatively easy. Such a current is not constant but fluctuates as a sine or cosine function of time.