Question

An $80\,kg$ person is parachuting and experiencing a downward acceleration of $2.5\,{m}/{{{s}^{2}}}$. The mass of the parachute is $5.0\,kg$.
(a) What is the upward force on the open parachute from the air?
(b) What is the downward force on the parachute from the person?

Answer 1

In order to answer the above question, we will draw a diagram to understand it. We will then draw the free body diagrams for both the cases and then try to write the equation of forces acting on the body. Keeping the desired force as a subject, we will find the answer corresponding to our question.

Complete step by step answer:
To understand the question properly, we will draw a simple diagram as follows:

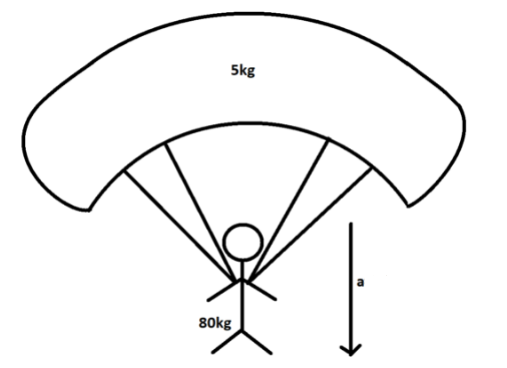
As we can see from the figure, we have a person having a mass of ${{m}_{1}}=80\,kg$ is parachuting in the sky and is accelerating downwards with an acceleration of $a=2.5\,{m}/{{{s}^{2}}}$. The mass of the parachute is ${{m}_{2}}=5\,kg$.

(a) We need to find the upward force of the open parachute from the air. Therefore, we can consider the above situation as a system having a total mass of $M={{m}_{1}}+{{m}_{2}}=80\,kg+5\,kg=85\,kg$ accelerating downwards with acceleration $a=2.5\,{m}/{{{s}^{2}}}$. Now, we draw a free body diagram for the following situation:

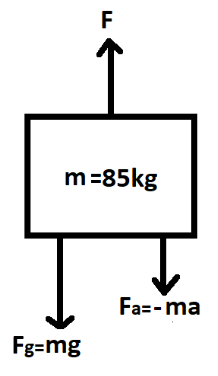
As we can see from the free body diagram, there are two forces acting in the downward direction. One of the forces is due to the gravitational acceleration${{F}_{g}}$ and the other is due to the downward acceleration${{F}_{a}}$ of the system. There is an upward force acting on the system which is due to the resistance of the parachute for downward acceleration $F$. The downward acceleration is negative as it is downward. (in contrast to the gravitational acceleration which is positive in downward direction)
Now, we write the equation of forces as:
$F={{F}_{g}}+{{F}_{a}}$
$\Rightarrow F=mg-ma \\\ \Rightarrow F=m(g-a) \\\$
Therefore, the upward force experienced by the parachute due to the system is
$F=85kg(9.8\dfrac{m}{{{s}^{2}}}-2.5\dfrac{m}{{{s}^{2}}}) \\\ \Rightarrow F=85(7.3) \\\ \Rightarrow F=620.5\,N \\\$
Therefore, the upward force acting on the parachute due to the system is $620.5\,N$.

(b) Now we need to find the downward force experienced by the parachute due to the person. We will first draw a free body diagram to understand such situation:

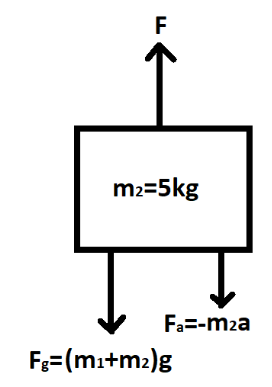
As we can see in the figure, the diagram is similar to the figure in the first part, the only difference is that we have to calculate the downward force acting on the parachute only due to the person and not by the whole system. Therefore, we take only the parachute as our system and calculate the forces acting on it.
Writing the equation of forces,
${{F}_{g}}+{{F}_{a}}=F$
$\Rightarrow ({{m}_{1}}+{{m}_{2}})g+({{m}_{2}})a=F$
As, we want to find the force due to the person
$\Rightarrow {{m}_{1}}g=F-({{m}_{2}})a-{{m}_{2}}g$
As we know the force acting upward on the parachute from the above calculation and also the acceleration is taken to be negative.
${{m}_{1}}g=F+({{m}_{2}})a-{{m}_{2}}g \\\ \Rightarrow {{m}_{1}}g=620.5+(5)2.5-(5)9.8 \\\ \Rightarrow {{m}_{1}}g=583N \\\$
Therefore, the force due to the person on the parachute is $583\,N$.

Note: It is very important to keep in mind that the acceleration due to gravity is positive in the downward direction whereas negative in the upward direction. Similarly, the acceleration on the system is negative in the downward direction whereas positive in the upward direction. It is also important to keep in mind what kind of force and force acting on whom is needed while doing the calculations.