Question

An $18\Omega ,9\Omega$ and $6\Omega$ resistors are connected in parallel to an emf source. A current of $4A$ is the $9\Omega$ resistor. How do you calculate the resistance of the circuit? What is the potential difference across the source?

Answer 1

To solve this question, we just need the basic concept of Ohm’s law and how to find the equivalent resistance for parallel combination. Here first we have calculated the potential difference across the source by simply applying the formula because we know when connection is parallel then potential difference is same for all the resistors. And then we calculated the resistance of the circuit by simply applying the formula and hence we got the required solution.

Formula used:
$V = IR$
Where,
$V$ is the voltage across the circuit,
$I$ is the current and
$R$ is the resistance.
Net resistance for parallel combination,

Complete step by step solution:

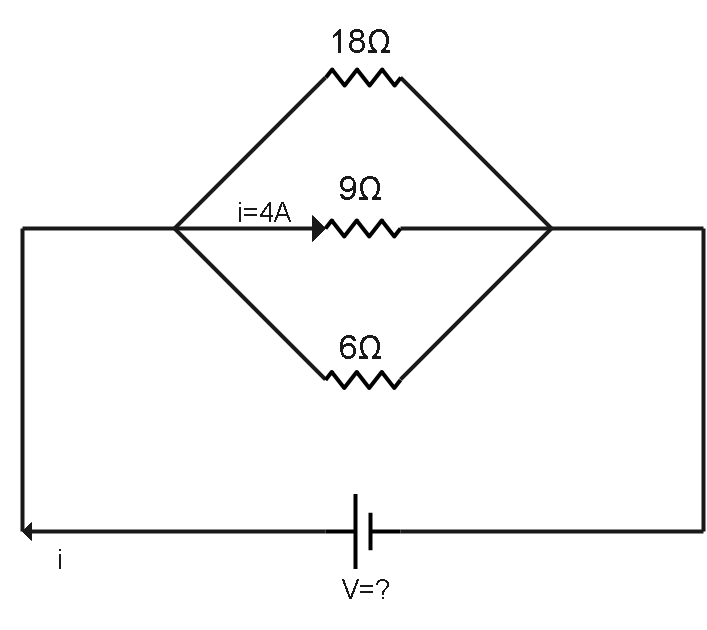
First let us calculate the potential difference across the source.
As we know that when the connection is parallel then the potential difference is the same for all the resistors.
And according to the question it is given,
Current on $9\Omega$ resistance is $4A$ .
So simply applying the Ohm’s law to calculate the potential difference,
i.e., $V = IR$
Therefore,

$$V = IR \\\ \Rightarrow V = 4 \times 9 \\\ \Rightarrow V = 36V \\\$$

Hence the potential difference across the source is $36V$ .
Now, calculating the resistance of the circuit as it is given that the circuit is parallel then simply applying resistance equivalent for parallel circuit,
i.e.,
Therefore,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{18}} + \dfrac{1}{9} + \dfrac{1}{6} \\\ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{1 + 2 + 3}}{{18}} \\\ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{6}{{18}} = \dfrac{1}{3} \\\ \Rightarrow {R_{eq}} = 3\Omega \\\$
Hence the resistance of the given circuit is $3\Omega$ .

Note:
When the connection is series then the current is the same for all the resistors.
When the connection is parallel then the potential difference is the same for all the resistors.
Students frequently mix up the equivalent resistance formula in parallel and series combinations, as well as the equivalent capacitance formula in series and parallel combinations. Students should also remember that a combination's equivalent resistance is always less than the parallel network's smallest resistance.