Question: Amudha walks at a speed of 3 kilometers per hour. Draw a linear graph to show the relationship betwe...

Question

Amudha walks at a speed of 3 kilometers per hour. Draw a linear graph to show the relationship between the time and distance.

Answer 1

Solution

In this question, we are given with the distance Amudha walks with respect to the time, hence to graph the solution we need to consider the given speed and time i.e., she walks at a speed of 3 km per hour, which implies that $3km \to 1hr$ , $6km \to 2hr$ and so on, hence based on this we need to plot the points and find the relationship between the time and distance.

Complete step by step solution:
Given,
Amudha walks at a speed of 3 kilometers per hour. It means she walks 3 Km in 1 hour, 6 Km in 2 hours, 9 km in 3 hours; i.e.,
$3km \to 1hr$ , $6km \to 2hr$ , $9km \to 3hr$ …... and so on.
Thus, we have the table according to the given data as:

Time in hours (x)	0	1	2	3	4	5
Distance in km (y)	0	3	6	9	12	15

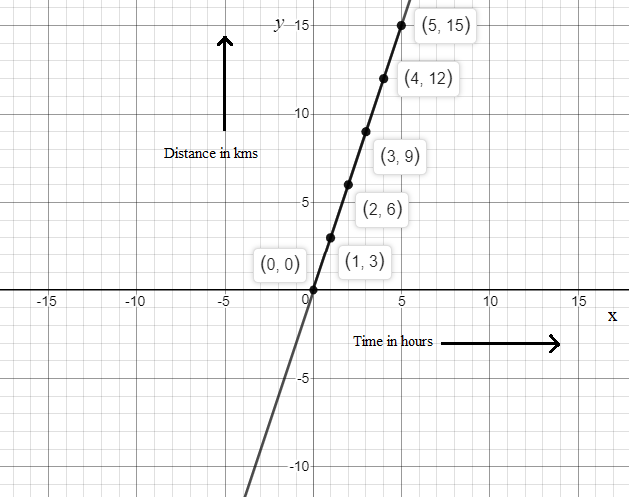
Hence, the points are: (0, 0), (1, 3), (2, 6), (3, 9), (4, 12) and (5, 15).
To graph the solution, plot the points (0, 0), (1, 3), (2, 6), (3, 9), (4, 12) and (5, 15) and join all these points, we get a straight line. Hence, it is a linear graph.
And to find the relationship between x and y: We know that,
$Dis\tan ce = Speed \times Time$
From the above table we have the relationship with respect to distance, speed and time is:
$Dis\tan ce = Speed \times Time$
$\to 0 = 3 \times 0$
$\to 3 = 3 \times 1$
$\to 6 = 3 \times 2$
$\to 9 = 3 \times 3$
$\to 12 = 3 \times 4$
$\to 15 = 3 \times 5$
Hence, we get the equation as:
$\Rightarrow y = 3x$
Here, y = Distance, x = Time in hour and 3 is the speed, hence the linear equation is $y = 3$ .

Note: We, must note the relationship Between Speed, Time & Distance as:
$Speed = \dfrac{{Dis\tan ce}}{{Time}}$ : This tells us how slow or fast an object moves. It describes the distance travelled divided by the time taken to cover the distance. Speed is directly Proportional to Distance and Inversely proportional to Time, Hence, $Dis\tan ce = Speed \times Time$ , and as the speed increases the time taken will decrease and vice versa i.e., $Time = \dfrac{{Dis\tan ce}}{{Speed}}$ .