Question

Among $800$ students, $220$ failed in Marathi, $300$ failed in English, $150$1 failed in Hindi, $125$ failed in both Marathi and English, $70$ failed in both Marathi and Hindi, $60$ failed in both English and Hindi, $30$ failed in all the three languages. Find the number of students who failed in
A.Two languages
B.Only one language
C.At least one language.

Answer 1

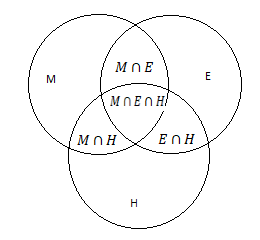
$A \cap B$ means the portion common in both A and B.$$$$
From the drawn venn diagram we will substitute the given values and add the respective values to find the answer of the given questions.

Complete step by step answer:
It is given that the total number of students is $800$.
$S = 800$.
And also the following terms are given.
$n(M) =$ the number of student failed in Marathi$= 220$
$n(E) =$ the number of student failed in English$= 300$
$n(H) =$ the number of student failed in Hindi$= 150$
$n(M \cap E) =$ the number of student failed in both Marathi and English $= 125$
$n(M \cap H) =$ the number of student failed in both Marathi and Hindi $= 70$
$n(E \cap H) =$ the number of student failed in both English and Hindi $= 60$
$n(M \cap H \cap E) =$ the number of student failed in all three languages $= 30$
The number of students who failed in two languages
To find the value we add the following data.
The number of students who failed in two languages = The number of student failed only in both Marathi and English+ the number of student failed only in both Marathi and Hindi + the number of student failed only in both English and Hindi + the number of student failed in all three languages
To find the value of students who failed in only two subjects we should subtract the number of students who failed in all three students from it.

$${ = \left( {125 - 30} \right) + \left( {70 - 30} \right) + \left( {60 - 30} \right) + 30} \\\ { = 95 + 40 + 30 + 30} \\\ { = 195}$$

The number of student failed only in Marathi $= n(M) - n(M \cap H) - n(M \cap E) + n(M \cap H \cap E)$
On substituting the given values we get,

$${ = 220 - 70 - 125 + 30} \\\ { = 55}$$

The number of student failed only in Hindi $= n\left( H \right) - n(M \cap H) - n(E \cap H) + {\text{ }}n(M \cap H \cap E)$
On substituting the given values we get,

$${ = 150 - 70 - 60 + 30} \\\ { = 50}$$

The number of student failed only in English $= n\left( E \right) - n(M \cap E) - n(E \cap H) + {\text{ }}n(M \cap H \cap E)$
On substituting the given values we get,

$${ = 300 - 125 - 60 + 30} \\\ { = 145}$$

Thus the number of students failed only in one language$= 55 + 50 + 145 = 250$.
The number of students who failed in at least one language=$n(M \cup H \cup E) = n\left( M \right) + n\left( H \right) + n\left( E \right) - {\text{ }}n(M \cap H) - n(M \cap E) - {\text{ }}n(E \cap H) + {\text{ }}n(M \cap H \cap E)$On substituting the given values we get,

$${ = 220 + 300 + 150 - 70 - 125 - 60 + 30} \\\ { = 445}$$

Hence, the number of students who failed in at least one language is 445.

Note:
Since we have to count the students who failed only in Marathi, from the Venn diagram we can see we need to exclude $M \cap H$ and $M \cap E$. For doing that we have excluded$M \cap H \cap E$ two times because it is the common area, so we will add it again. Similarly for the other two languages we have proceeded the same.