Question

Ammeter and voltmeter readings were recorded as 0.25A and 0.5V during the experiment to determine the resistance of a given wire using Ohm’s law. The correct value of the resistance is.

Answer 1

Remember that, ammeter is used to measure current and voltmeter for measuring voltage across two points. Hence, we get the values of the voltage and current directly from the question. Now you could recall Ohm’s law and then substitute the given values to get resistance.

Formula used:
Ohm’s law,
$V=IR$

Complete step by step answer:
In every field of physics, we have certain equations that we use so often that it becomes by-heart to us. Ohm’s law is one such equation. This law was named after Georg Ohm who was a German physicist. Ohm’s law states that, the voltage difference between two points is directly proportional to current through a conductor between these two points. That is,
$V\propto I$
$V=IR$ …………………. (1)
Where, R is the constant of proportionality called the resistance. Resistance, by definition, is the opposition offered by the circuit to the flow of current. The SI unit of resistance is Ohm represented by the Greek symbol-$\Omega$. You should note that the R here in his relation is constant, that is it is independent of the current.
Let us now look at the circuit used in experimental setup for proving Ohm’s law.

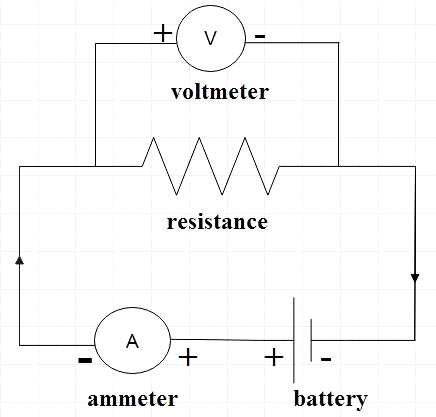
Though we now consider Ohm’s law quite obvious, there was a time when this law was very important among quantitative descriptions of the physics of electricity.
In the question, we are given the readings taken during an experiment based on Ohm’s law. We have readings from ammeter and voltmeter as 0.25A and 0.5V respectively. That is,
Voltage V as per voltmeter reading is,
$V=0.5V$
Current I as per the ammeter reading is,
$I=0.25A$
We could now substitute these values in equation (1).
$R=\dfrac{V}{I}=\dfrac{0.5V}{0.25A}$
$R=2\Omega$
Therefore, we get the resistance in the circuit as $2\Omega .$

Note:
If you knew ammeter and voltmeter is used to measure current and voltage respectively then this question is a very simple substitution problem. In addition, you have to know Ohm’s law to solve this problem which may be by heart now by heart for you. Since volt (V) and ampere (A) are the SI units of voltage and current respectively, you will directly get the resistance in its SI unit, that is, Ohm$\left( \Omega \right)$.