Question

Aluminium crystallizes in an FCC structure. Atomic radius of the metal is 125pm. What is the length of the side of the unit cell of the metal?

Answer 1

Face centered cubic [FCC] crystal structure has eight spheres at corner of cube and one sphere at center of each face of cube.

Formula used: $a = \sqrt 8 r$

Complete step by step answer: The FCC structure is given as:

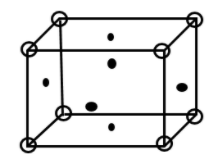
Given that aluminium crystallizes in FCC structure.
Therefore, we first calculate No. of molecules present in FCC structure.
8 molecules present at corner of cube therefore No. of molecule at corner$= \dfrac{1}{8} \times 8$
6 molecules present on face of cube therefore No. of molecule at faces$= \dfrac{1}{2} \times 6$ = 3
Total molecule = 3 + 1= 4

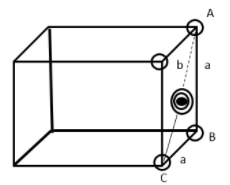
Consider triangle ABC of a side of a face centered cubic unit cell.
The length of edge = a
Hypotenuse AC = b
By Pythagoras theorem
$A{C^2} = A{B^2} + B{C^2}$
${b^2} = {a^2} + {a^2}$
${b^2} = 2{a^2}$ . . . . . (1)
Since $b = 4r$ $r =$radius of sphere.
Hypotenuse b has one sphere and two half spheres
Putting value of b in equation (1)
${\left( {4r} \right)^2} = 2{a^2}$
$16{r^2} = 2{a^2}$
${a^2} = \dfrac{{16{r^2}}}{2} = 8{r^2}$
$\therefore a = \sqrt 8 r$
In given problem $r = 125pm.$
So length of side of unit cell is
$a = \sqrt 8 \times 125$
$\sqrt 8 = \sqrt {4 \times 2}$
$= 2\sqrt 2$
$a = 2\sqrt 2 \times 125$
$\sqrt 2 = 1.414$
$a = 2 \times 1.414 \times 125$
a = 353.5pm

Therefore, the edge length of face centered cubic structure of aluminium is 353.5 pm.

Note: The relation between edge length of crystal structure and radius of sphere is different in different structures. This is as follows.
Simple cubic a = 2r
Face centered cubic[FCC] $a = \sqrt 8 r$
Body centered cubic[BCC] $a = \dfrac{{4r}}{{\sqrt 3 }}$