Question

Aluminium crystallises in an FCC structure. Atomic radius of the metal is 125 pm. Calculate the edge length of the unit cell of the metal.

Answer 1

The pre-knowledge of unit cells and crystal lattice will help us solve this problem. The relationship between atomic radius and the edge length of a unit cell can be derived for FCC structure to illustrate the given data.

Complete answer:
Let us learn about the crystal lattice and its types;
Crystal lattice- The arrangement of atoms or ions in the three-dimensional form in a crystal.
Unit cell- A unit cell is the smallest repeating unit of a crystal lattice.
Types of unit cell-
1. Simple cubic structure
2. Body centred cubic structure
3. Face centred cubic structure
Let us concentrate on the third type of a unit cell i.e. FCC structure;
-The FCC unit cell consists of the atoms at all the corners of the crystal and at the centre of all the faces of the cube.
-Thus, total 4 atoms are present in an FCC unit cell. As,
a. Corners of a cube- $8\times \dfrac{1}{8}=1$ atom.
b. Faces of a cube- $6\times \dfrac{1}{2}=3$ atoms.
-As, we know that FCC have an atom in the middle of each face of the cube, this can be represented by the following diagram,

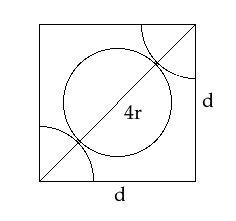
To find the relationship between the edge length of the cube and the radius of an atom, apply Pythagoras theorem to above given figure;
$\begin{aligned} & Sid{{e}_{1}}^{2}+Sid{{e}_{2}}^{2}=Hypotenuse{{s}^{2}} \\\ & {{d}^{2}}+{{d}^{2}}={{\left( 4r \right)}^{2}} \\\ & \sqrt{2}d=4r \\\ & \therefore d=2\sqrt{2}r \\\ \end{aligned}$
Thus, by using this relationship for solving the given illustration, we get,
Given that,
Radius of metal = 125 pm
Thus, edge length can be given as,
$\begin{aligned} & d=2\sqrt{2}\times 125pm \\\ & d=353.55pm \\\ \end{aligned}$

Therefore, the edge length of a unit cell in an FCC structure is 353.55 pm.

Note: Here, pm is a unit of length i.e. picometer. Also, the relationship between the atomic radius and edge length is different for all types of unit cells; each one has its own significance.