Question

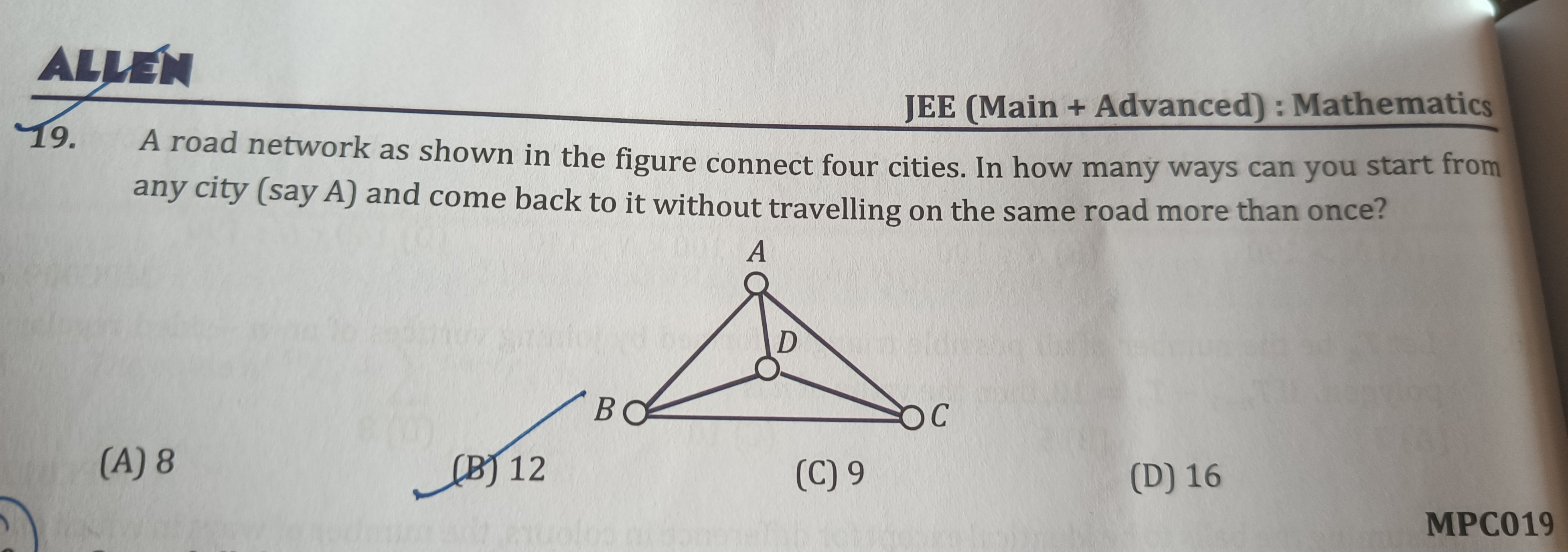
A road network as shown in the figure connect four cities. In how many ways can you start from any city (say A) and come back to it without travelling on the same road more than once?

• A. 8
• B. 12
• C. 9
• D. 16

Answer 1

Answer: (B)

12

Answer 2

The problem asks for the number of ways to start from a city (say A) and come back to it without travelling on the same road more than once. This is a problem of finding the number of simple cycles in a graph that start and end at a specific vertex, say A.

The given figure shows a road network connecting four cities, A, B, C, and D. Let's represent the cities as vertices and the roads as edges in a graph. The connections are:

• A is connected to B, C, D (AB, AC, AD)
• B is connected to A, C, D (BA, BC, BD)
• C is connected to A, B, D (CA, CB, CD)
• D is connected to A, B, C (DA, DB, DC)

This means the graph is a complete graph with 4 vertices, denoted as $K_4$.

We need to find the number of distinct directed simple cycles that start and end at vertex A. A simple cycle does not repeat any vertex (except the starting/ending vertex) and does not repeat any edge.

In a graph with $n$ vertices, the maximum length of a simple cycle is $n$. Here, $n=4$. So, the possible lengths of simple cycles starting and ending at A are 3 and 4.

1. Cycles of Length 3 (Triangles containing A):

These cycles involve A and two other cities. The possible triangles involving A are:

• Triangle A-B-C:
  • A $\to$ B $\to$ C $\to$ A
  • A $\to$ C $\to$ B $\to$ A
• Triangle A-B-D:
  • A $\to$ B $\to$ D $\to$ A
  • A $\to$ D $\to$ B $\to$ A
• Triangle A-C-D:
  • A $\to$ C $\to$ D $\to$ A
  • A $\to$ D $\to$ C $\to$ A

Each triangle containing A gives 2 distinct directed cycles starting and ending at A. Since there are 3 such triangles, the total number of cycles of length 3 is $3 \times 2 = 6$.

2. Cycles of Length 4 (Hamiltonian Cycles containing A):

These cycles must visit all four cities (A, B, C, D) exactly once and return to A. For a complete graph $K_n$, the number of Hamiltonian cycles starting and ending at a specific vertex is $(n-1)!$. For $K_4$, $n=4$, so the number of Hamiltonian cycles starting and ending at A is $(4-1)! = 3! = 3 \times 2 \times 1 = 6$.

Let's list them explicitly:

• A $\to$ B $\to$ C $\to$ D $\to$ A
• A $\to$ B $\to$ D $\to$ C $\to$ A
• A $\to$ C $\to$ B $\to$ D $\to$ A
• A $\to$ C $\to$ D $\to$ B $\to$ A
• A $\to$ D $\to$ B $\to$ C $\to$ A
• A $\to$ D $\to$ C $\to$ B $\to$ A

All 6 of these cycles are distinct.

Total Number of Ways:

The total number of ways to start from city A and come back to it without travelling on the same road more than once is the sum of cycles of length 3 and cycles of length 4.

Total ways = (Number of length 3 cycles) + (Number of length 4 cycles)

Total ways = $6 + 6 = 12$.