Question

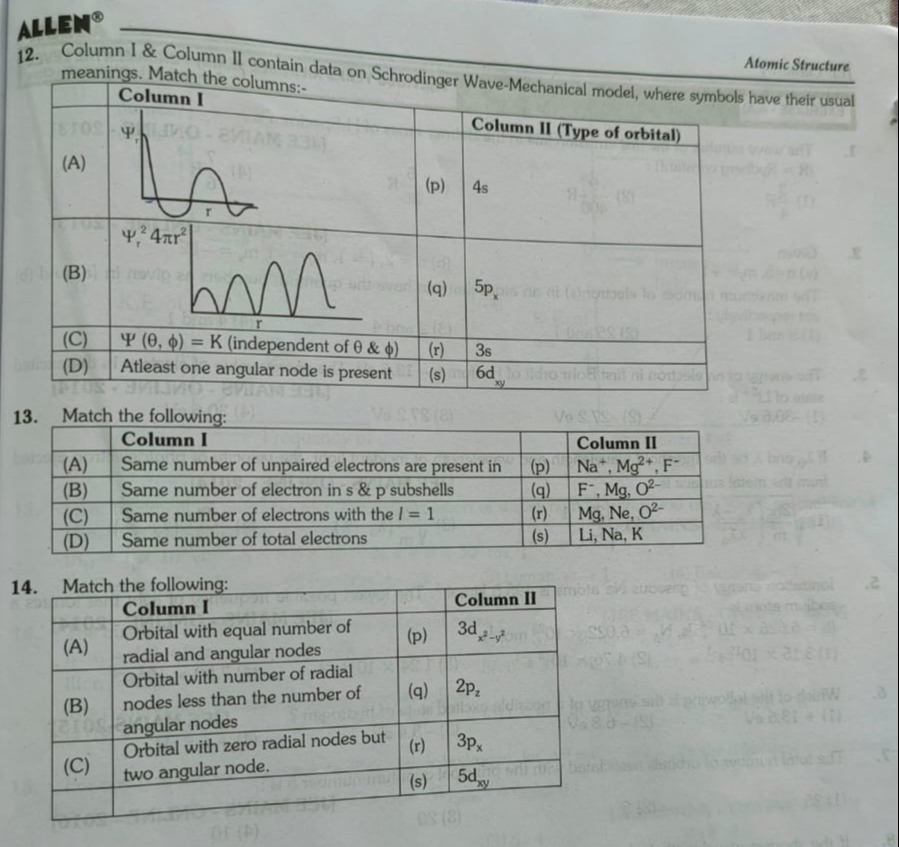
Column I & Column II contain data on Schrodinger Wave-Mechanical model, where symbols have their usual meanings. Match the columns:-

	Column I		Column II (Type of orbital)
(A)		(p)	4s
	$\psi_r^2 4\pi r^2$
(B)		(q)	$5p_x$
(C)	$\Psi (\theta, \phi) = K$ (independent of $\theta$ & $\phi$)	(r)	3s
(D)	Atleast one angular node is present	(s)	$6d_{xy}$

• A. A - r
• B. B - q
• C. C - p
• D. D - s

Answer 1

A - r, B - q, C - p, D - s

Answer 2

Question 12:

• (A) $\psi_r$ vs r graph: The graph shows 2 radial nodes (where $\psi_r$ crosses the r-axis). For a 3s orbital (n=3, l=0), the number of radial nodes is $n-l-1 = 3-0-1 = 2$.
• (B) $\psi_r^2 4\pi r^2$ vs r graph: The graph shows 3 radial nodes (where the probability density is zero) and 4 peaks. For 5p orbital (n=5, l=1), radial nodes = $5-1-1=3$, and number of peaks = $n-l=5-1=4$.
• (C) $\Psi(\theta, \phi) = K$: This implies the angular part of the wave function is constant, meaning it is spherically symmetric. This is characteristic of s-orbitals (l=0). The 4s orbital is the only remaining s-orbital option.
• (D) At least one angular node: An angular node is present when $l \ge 1$. The 6d$_{xy}$ orbital has $l=2$, hence it has two angular nodes (which is at least one).