Question

All x satisfy the inequality
${{\left( {{\cot }^{-1}}x \right)}^{2}}-7\left( {{\cot }^{-1}}x \right)+10>0$, lie in the interval
(a) $\left( -\infty ,\cot 5 \right)\cup \left( \cot 4,\cot 2 \right)$
(b) $\left( \cot 5,\cot 4 \right)$
(c) $\left( \cot 2,\infty \right)$
(d) $\left( -\infty ,\cot 2 \right)\cup \left( \cot 5,\infty \right)$

Answer 1

Hint: First of all, let ${{\cot }^{-1}}x=y$ and resolve the equation into factors and find the range of $y={{\cot }^{-1}}x$. Then draw the graph of ${{\cot }^{-1}}x$ to examine the values of x. Consider the domain and range of ${{\cot }^{-1}}x$ properly for the correct values of x.

Complete step-by-step answer:
We are given that ${{\left( {{\cot }^{-1}}x \right)}^{2}}-7\left( {{\cot }^{-1}}x \right)+10>0$.
Here, we have to find the values of x which satisfies this inequality.

Let us consider the inequality given in the question.
${{\left( {{\cot }^{-1}}x \right)}^{2}}-7\left( {{\cot }^{-1}}x \right)+10>0$
Let us consider ${{\cot }^{-1}}x$ to be y. By substituting ${{\cot }^{-1}}x=y$ in the above inequality, we get,
${{y}^{2}}-7y+10>0$

Here, we can write 7y = 5y + 2y. So, we get,
${{y}^{2}}-5y-2y+10>0$
We can write the above inequality as,
$y\left( y-5 \right)-2\left( y-5 \right)>0$
By taking out (y – 5) common, we get,
$\left( y-5 \right)\left( y-2 \right)>0$

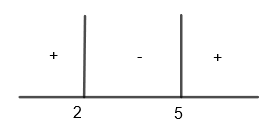
If y > 5, then (y – 5) > 0 and (y – 2) > 0.
So, we get (y – 5) (y – 2) > 0

Hence, y > 5 satisfies the inequality.
For example, let us take y = 7. By substituting y = 7, we get,
$\left( 7-5 \right)\left( 7-2 \right)=\left( 2 \right)\left( 5 \right)=10>0$
So, we get, $y\in \left( 5,\infty \right)$.
If 2 < y < 5, then (y – 5) < 0 and (y – 2) > 0
So, we get (y – 5) (y – 2) < 0

Hence, 2 < y < 5 does not satisfy the inequality.

For example, let us take y = 3. By substituting y = 3, we get,
$\left( 3-5 \right)\left( 3-2 \right)=\left( -2 \right)\left( 1 \right)=-2<0$
So, we get, $y\notin \left( 2,5 \right)$.
If y < 2, then (y – 5) < 0 and (y – 2) < 0.
So, we get, (y – 5) (y – 2) > 0

Hence y < 2 satisfies the inequality.
For example, let us take y = 0. By substituting y = 0, we get,
$\left( 0-5 \right)\left( 0-2 \right)=\left( -5 \right)\left( -2 \right)=10>0$
So, we get $y\in \left( -\infty ,2 \right)$.
Hence, we get $y\in \left( -\infty ,2 \right)\cup \left( 5,\infty \right)$.
We had assumed that ${{\cot }^{-1}}x=y$, so by substituting $y={{\cot }^{-1}}x$, we get,
${{\cot }^{-1}}x\in \left( -\infty ,2 \right)\cup \left( 5,\infty \right)$
So, we get ${{\cot }^{-1}}x<2$ and ${{\cot }^{-1}}x>5$.

Now, we will see the graph of ${{\cot }^{-1}}x$, that is

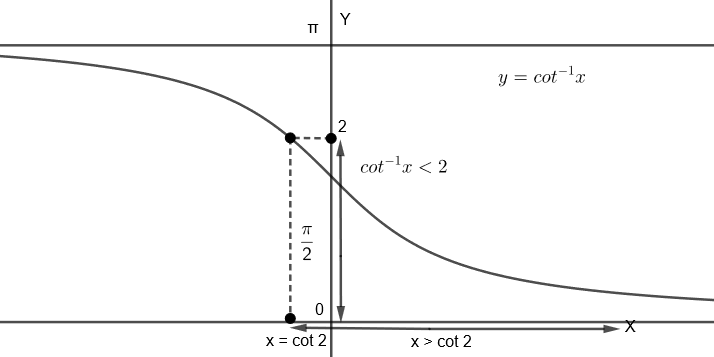
We know that the range of ${{\cot }^{-1}}x$ is $\left( 0,\pi \right)$, so it can’t be greater than 5.

Now, considering ${{\cot }^{-1}}x<2$
From the graph, we can see that, for ${{\cot }^{-1}}x<2,\text{ }x>\cot 2$
So, we get $x\in \left( \cot 2,\infty \right)$.

Hence, the correct answer is option (c).

Note: After getting ${{\cot }^{-1}}x\in \left( -\infty ,2 \right)\cup \left( 5,\infty \right)$, students often make this mistake of calculating x as $x\in \left( -\infty ,\cot 2 \right)\cup \left( \cot 5,\infty \right)$ but this is wrong as we know that ${{\cot }^{-1}}x$ could not be greater than 5 because its range is $\left( 0,\pi \right)$. Also for ${{\cot }^{-1}}x\in \left( -\infty ,2 \right)$, $x\in \left( \cot 2,\infty \right)$ not $\left( -\infty ,\cot 2 \right)$. So for inverse trigonometric function, it is advisable to first draw the graph and then only examine the values of x for the correct results.