Question
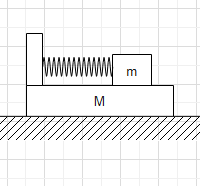
Question: All the surfaces shown in the figure are frictionless. The mass of the car is M, that of the block i...
All the surfaces shown in the figure are frictionless. The mass of the car is M, that of the block is m and the spring has spring constant k. Initially, the car and the block are at rest and the spring is stretched through a length, when the system is released.
(a) Find the amplitude of the simple harmonic motion of the block and of the car as seen from the road.
(b) Find the time period(s) of the two simple harmonic motions.
Solution
The sum of the amplitudes of the car and the block will be equal to the maximum extension of the spring. Then use the law of conservation of momentum and find the relation between the masses and the amplitudes. For the time periods use the formula for the time period of simple harmonic motion.
Complete answer:
(a) The amplitude of the block and the car will depend on the extension of the spring. When stretched or compressed to maximum, the block and the car will have the maximum displacements. The maximum displacements of the block and the car are their amplitudes.
Let the amplitudes of the car and the block be A1 and A2 respectively.
It is given that the spring is stretched by a length x0 and this is the maximum extension in the spring. Therefore,
x0=A1+A2 …. (i).
When the system is released, spring will apply force on the two objects which will be equal to F= kx directed in the opposite direction of the displacement of the objects.
Here, x is the change in the original length of the spring.
In this case, the two spring forces will be equal in magnitude but opposite in directions. Therefore, the net force on the system is zero.
When the net force acting on a system is zero, the net momentum of the system will be constants.
In other words, we can say that the momentum of the centre mass of the system will be constant. We know that the centre of mass of the system is at rest initially. Therefore, the momentum of the system will zero throughout the motion.
This means that the centre of mass of the system is always at rest.
Now displacement of the centre of mass of two bodies is given as xcom=m1+m2m1x1+m2x2
In this case, m1=M and m2=m and xcom=0.
Therefore,
0=M+mMx1+mx2
⇒Mx1+mx2=0
When the car and the block are displaced by A1 and A2,
⇒MA1+mA2=0
⇒MA1=−mA2
If we only consider the magnitudes, then MA1=mA2.
⇒A1=MmA2
Substitute this value in (i).
⇒x0=(MmA2)+A2
⇒x0=(Mm+1)A2
⇒x0=(Mm+M)A2
⇒A2=M+mMx0.
Substitute this value in (i)
⇒x0=A1+M+mMx0
⇒A1=M+mmx0.
Therefore, the amplitude of the car is A1=M+mmx0.
And the amplitude of the block is A2=M+mMx0.
(b) The time period of a body of mass m under simple harmonic motion is given as T=2πkm.
Therefore, the time period of the car is T1=2πkM.
And the time period of the block is T2=2πkm.
Note:
If you find the given system of a car and a block, then you can replace the system with a system of two blocks of masses M and m lying on with a spring attached in between them. This is because all the surfaces are frictionless.
