Question

All the resistance in the figure is in ohms. The effective resistance between points A and B is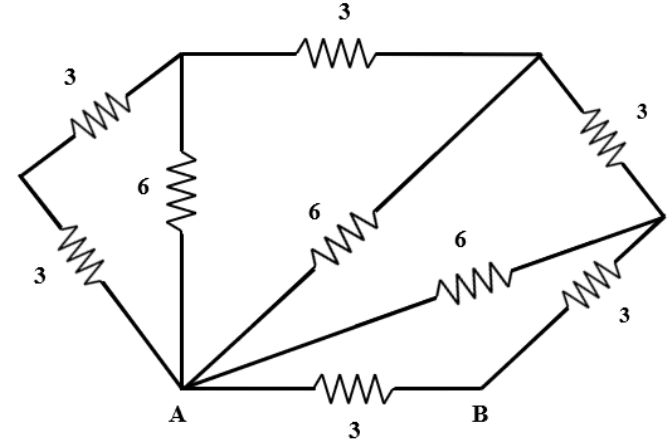

A. 6 ohms
B. 3 ohms
C. 9 ohms
D. 2 ohms

Answer 1

To solve this problem, use the formula for equivalent resistance when resistors are connected in series and also the formula for equivalent resistance when resistors are connected in parallel. Find the equivalent resistance of the first network then combine it with resistance of another network. Find the equivalent resistance of both the networks combined. Similarly, find the equivalent resistance of each network and find the effective resistance between points A and B.
Formula used:
$\dfrac {1}{{R}_{eq}}= \dfrac {1} {{R}_{1}} + \dfrac {1}{{R}_{2}}+ \dfrac {1}{{R}_{3}}+ …+\dfrac {1}{{R}_{N}}$
${R}_{eq}= {R}_{1}+{R}_{2}+{R}_{3}+…+{R}_{N}$

Complete step-by-step solution:

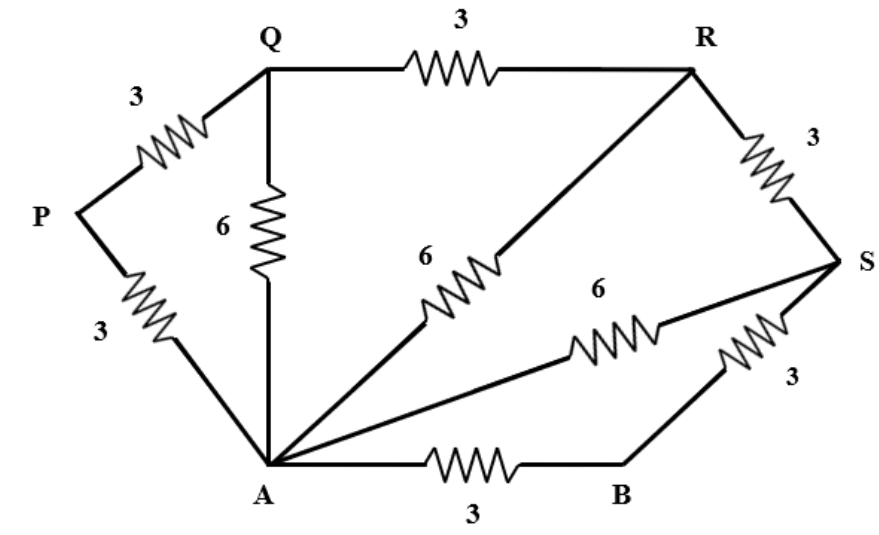
In the above labelled diagram, we can see the resistors AP and PQ are in series. So, their equivalent resistance will be,
${R}_{eq1}= 3 + 3$
$\Rightarrow {R}_{eq1}= 6\Omega$
Now, the ${R}_{eq1}$ connected in parallel with the resistor AQ. So, their equivalent resistance is given by,
$\dfrac {1}{{R}_{eq2}}= \dfrac {1}{{R}_{eq1}}+ \dfrac {1}{{R}_{AQ}}$
Substituting values in above equation we get,
$\dfrac {1}{{R}_{eq2}}= \dfrac {1}{6}+ \dfrac {1}{6}$
$\Rightarrow \dfrac {1}{{R}_{eq2}}=\dfrac {12}{36}$
$\Rightarrow {R}_{eq2}= \dfrac {36}{12}$
$\Rightarrow {R}_{eq2}= 3\Omega$
Now, ${R}_{eq2}$ is in series with the resistor QR. So, their equivalent resistance is given by,
${R}_{eq3}= {R}_{eq2}+ {R}_{QR}$
Substituting the values in above equation we get,
${R}_{eq3}= 3 + 3$
$\Rightarrow {R}_{eq3}= 6\Omega$
Now, the ${R}_{eq3}$ connected in parallel with the resistor AR. So, their equivalent resistance is given by,
$\dfrac {1}{{R}_{eq4}}= \dfrac {1}{{R}_{eq3}}+ \dfrac {1}{{R}_{AR}}$
Substituting values in above equation we get,
$\dfrac {1}{{R}_{eq4}}= \dfrac {1}{6}+ \dfrac {1}{6}$
$\Rightarrow \dfrac {1}{{R}_{eq4}}=\dfrac {12}{36}$
$\Rightarrow {R}_{eq4}= \dfrac {36}{12}$
$\Rightarrow {R}_{eq4}= 3\Omega$
Now, ${R}_{eq4}$ is in series with the resistor RS. So, their equivalent resistance is given by,
${R}_{eq5}= {R}_{eq4}+ {R}_{RS}$
Substituting the values in above equation we get,
${R}_{eq5}= 3 + 3$
$\Rightarrow {R}_{eq5}= 6\Omega$
Now, the ${R}_{eq5}$ connected in parallel with the resistor AS. So, their equivalent resistance is given by,
$\dfrac {1}{{R}_{eq6}}= \dfrac {1}{{R}_{eq5}}+ \dfrac {1}{{R}_{AS}}$
Substituting values in above equation we get,
$\dfrac {1}{{R}_{eq6}}= \dfrac {1}{6}+ \dfrac {1}{6}$
$\Rightarrow \dfrac {1}{{R}_{eq6}}=\dfrac {12}{36}$
$\Rightarrow {R}_{eq6}= \dfrac {36}{12}$
$\Rightarrow {R}_{eq6}= 3\Omega$
Now, ${R}_{eq6}$ is in series with the resistor SB. So, their equivalent resistance is given by,
${R}_{eq7}= {R}_{eq6}+ {R}_{SB}$
Substituting the values in above equation we get,
${R}_{eq7}= 3 + 3$
$\Rightarrow {R}_{eq7}= 6\Omega$
Now, the ${R}_{eq7}$ connected in parallel with the resistor AB. So, their equivalent resistance is given by,
$\dfrac {1}{{R}_{eq8}}= \dfrac {1}{{R}_{eq7}}+ \dfrac {1}{{R}_{AB}}$
Substituting values in above equation we get,
$\dfrac {1}{{R}_{eq8}}= \dfrac {1}{6}+ \dfrac {1}{3}$
$\Rightarrow \dfrac {1}{{R}_{eq8}}=\dfrac {9}{18}$
$\Rightarrow {R}_{eq8}= \dfrac {18}{9}$
$\Rightarrow {R}_{eq8}= 2\Omega$
Hence, the effective resistance between points A and B is 2 ohms. So, the correct answer is option D i.e. 2 ohms.

Note: Students should remember that the equivalent resistance of a combination is always less than the smallest resistance in the parallel network. As we add more resistors in the network, the total resistance of the circuit will always decrease. While, in a series network, the equivalent resistance of the network is greater than the value of the largest resistor in the chain. The current flowing through each parallel branch may not be the same. But the voltage across each resistor in a parallel network is always the same.