Question
Question: All the elements of a square matrix A of order 'n' are non-negative. If $a_{ij} \forall i \neq j$, i...
All the elements of a square matrix A of order 'n' are non-negative. If aij∀i=j, is the least non-negative value of the function, f(x)=x2+2x−1 and tr(A) = λ, then maximum value of |A| will be
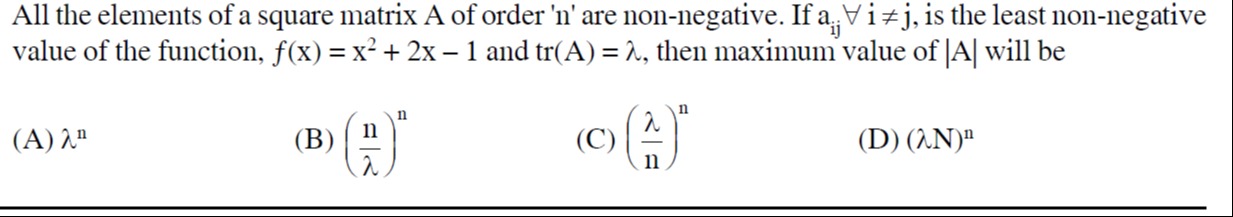
λn
(λn)n
(nλ)n
(λN)n
(nλ)n
Solution
The given function is f(x)=x2+2x−1. We need to find its least non-negative value. f(x)=(x2+2x+1)−1−1=(x+1)2−2. The minimum value of f(x) is -2, which occurs at x=−1. We are looking for the least non-negative value, i.e., the smallest value of f(x) such that f(x)≥0. We solve f(x)=0: x2+2x−1=0. Using the quadratic formula, x=2(1)−2±22−4(1)(−1)=2−2±8=−1±2. The roots are x1=−1−2 and x2=−1+2. Since the parabola opens upwards, f(x)≥0 when x≤−1−2 or x≥−1+2. The values of f(x) range from -2 upwards. The smallest non-negative value that f(x) takes is 0, which occurs at x=−1+2 and x=−1−2.
The off-diagonal elements of the matrix A, aij for i=j, are equal to this least non-negative value. So, aij=0 for all i=j. This means the matrix A is a diagonal matrix: A=a110⋮00a22⋮0⋯⋯⋱⋯00⋮ann
All elements of A are non-negative, so aii≥0 for all i. The trace of A is given by tr(A) = ∑i=1naii=λ. The determinant of a diagonal matrix is the product of its diagonal elements: ∣A∣=∏i=1naii=a11a22⋯ann.
We want to maximize the product P=a11a22⋯ann subject to the constraints aii≥0 for all i and ∑i=1naii=λ. By the Arithmetic Mean - Geometric Mean (AM-GM) inequality, for non-negative numbers a11,a22,…,ann: na11+a22+⋯+ann≥na11a22⋯ann Substituting the sum: nλ≥(∣A∣)1/n Raising both sides to the power of n (since n is a positive integer): (nλ)n≥∣A∣
The maximum value of ∣A∣ is (nλ)n. This maximum is achieved when the equality in the AM-GM inequality holds, which is when a11=a22=⋯=ann. If aii=c for all i, then ∑i=1nc=nc=λ, so c=nλ. Since all elements of A are non-negative, aii=λ/n must be non-negative. As λ is the sum of non-negative numbers, λ≥0. Since n is the order of the matrix, n≥1. Thus, λ/n≥0 is valid.
The maximum value of ∣A∣ is (nλ)n.
