Question
Question: All surfaces shown in figure are smooth system is released with the spring unstretched In equilibriu...
All surfaces shown in figure are smooth system is released with the spring unstretched In equilibrium, compression in the spring will be
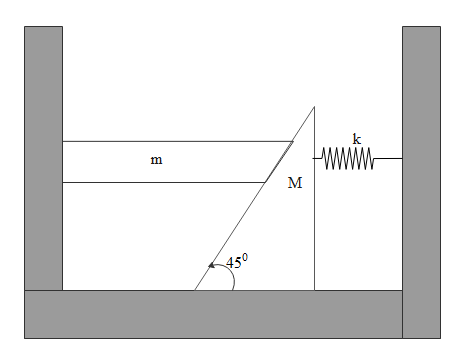
A. 2kmg
B. k2mg
C. 2k(m+M)g
D. kmg
Solution
When a wedge is connected to the string and when it was given that the system is in equilibrium then here must be some force that balances the spring force on the wedge and that force will be the component of normal exerted by mass m on the wedge. The mass m is also in equilibrium.
Complete step by step answer:
Here if we see the diagram clearly, the mass m is constrained to move only in the vertical direction, because in the horizontal direction the normal forces from the wall and the component of normal force from the wedge will be balanced each other and there will be no motion along the horizontal direction.
At the instant where the vertical component of normal force on mass ‘m’ gets balanced with its weight, the vertical motion of mass ‘m’ will be stopped.
We are asked to find out the compression in the spring in equilibrium condition, which means neither wedge nor mass ‘m’ should move.
If we clearly observe the below given diagram
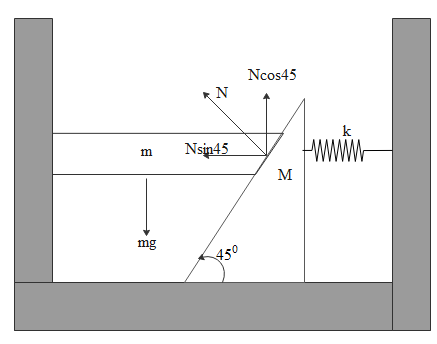
The weight of the mass ‘m’ will be acting downwards and is given by mg. It will be balanced by upward normal component.
F=ma where ‘F’ is the force acting and ‘a’ is the acceleration and ‘m’ is the mass.
So
\eqalign{
& N\cos {45^0} = mg \cr
& \Rightarrow N = \sqrt 2 mg \cr}
Now the same normal force will be acting on the wedge too. The horizontal component of normal force on the wedge will be Nsin450
That horizontal component will be equal to the spring force which will be Fs=kx
So we have
\eqalign{
& N\sin {45^0} = kx \cr
& \Rightarrow \dfrac{{\sqrt 2 mg}}{{\sqrt 2 }} = kx \cr
& \therefore x = \dfrac{{mg}}{k} \cr}
Hence answer would be option D.
Note:
So the spring keeps on compressing until the vertical motion of the mass ‘m’ and the horizontal motion of the wedge stops. Here the normal force will be varying from the starting to equilibrium position and simultaneously the spring force also will be varying. The shape at the end of the mass ‘m’ is tapered in a way it makes 45 degrees with the horizontal so that normal reaction will be exactly perpendicular to the wedge and the mass ‘m’.
