Question

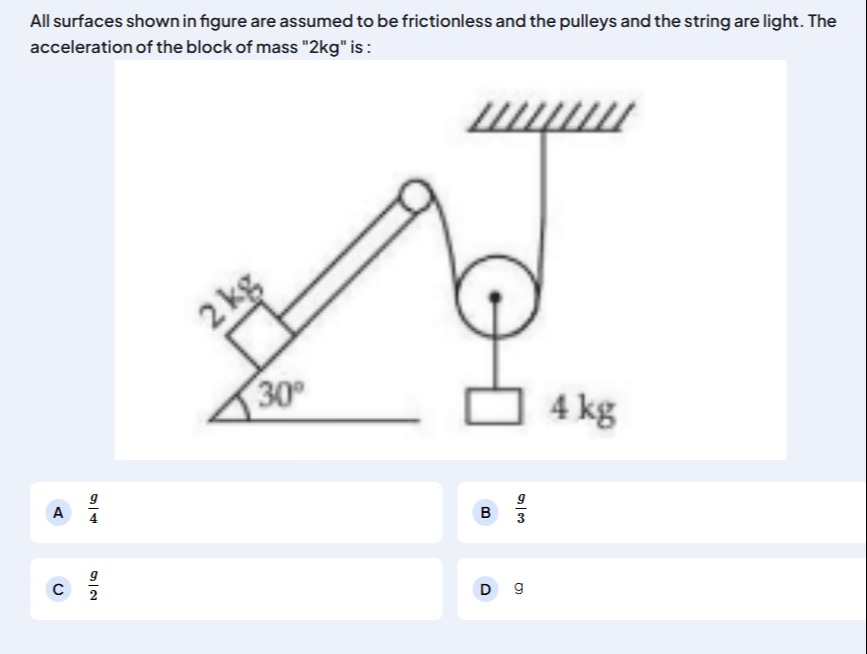
All surfaces shown in figure are assumed to be frictionless and the pulleys and the string are light. The acceleration of the block of mass "2kg" is:

• A. $\frac{g}{4}$
• B. $\frac{g}{3}$
• C. $\frac{g}{2}$
• D. g

Answer 1

Answer: (C)

$\frac{g}{2}$

Answer 2

Let $a_1$ be the acceleration of the 2kg block up the incline and $a_2$ be the acceleration of the 4kg block downwards. The string has tension $T$.

For the 2kg block ($m_1 = 2$ kg): The forces along the incline are tension $T$ upwards and the component of gravity $m_1g \sin(30^\circ)$ downwards. The equation of motion is $T - m_1g \sin(30^\circ) = m_1a_1$. $T - 2g \times \frac{1}{2} = 2a_1 \implies T - g = 2a_1$. (1)

For the 4kg block ($m_2 = 4$ kg): This is a movable pulley system. The relation between accelerations is $a_1 = a_2$. Let $a = a_1 = a_2$.

The equation of motion for the 4kg block is $m_2g - T = m_2a_2$. $4g - T = 4a$. (2)

From (1): $T = g + 2a$. Substitute $T$ into (2): $4g - (g + 2a) = 4a$. $3g = 6a$. $a = \frac{g}{2}$.