Question

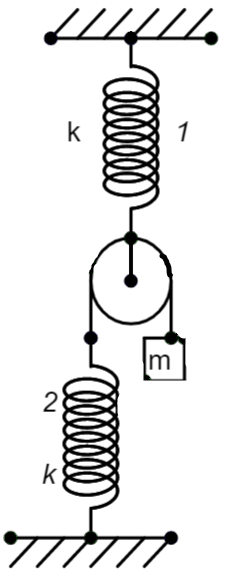
All springs, string, and pulley shown in the figure are light, initially when both the strings were in their natural state, the system was released from the rest. The maximum displacement of the block is $x\times (\dfrac{5mg}{k})$. Calculate x.

Answer 1

We need to understand the relation between the two springs on a pulley and the mass hanging on the system with the velocity it may attain once the system is set to motion. The relation can get us the idea of the unknown variable in the problem.

Complete step-by-step solution
We are given a system of springs as given in the figure. We know that the mass ‘m’ hanging from the pulley can extend both the springs. The extension of each of the springs is dependent on the position of the spring in the arrangement.
We know that the extension of spring 1 will be the result of the mass and the extension of spring 2. If ‘a’ is the extension of spring 1 in the system and ‘b’ be the extension on spring 2. When spring 2 is extended, the mass goes in a downward direction for ‘b’ displacement. When spring 2 is released, the total displacement will be twice its displacement, thus becoming ‘2b’.
The mass displaces in both directions with the same quantity as that of spring 1.
The net displacement of the mass can be given as –
$y=a+2b$
Now, let us balance the force due to the mass and the force due to the extension of the spring in the two cases. The springs have a spring constant of ‘k’ and a mass ‘m’ is attached to the pulley connected to spring 2 through a wire.

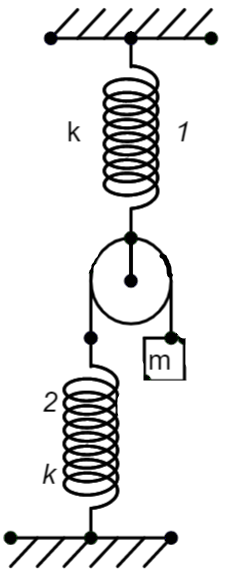
For the spring 1 –

& mg=ka \\\ & \therefore a=\dfrac{mg}{k} \\\ \end{aligned}$$ For the spring 2 – $$\begin{aligned} & mg+ka=kb \\\ & \Rightarrow mg+k(\dfrac{mg}{k})=kb \\\ & \therefore b=\dfrac{2mg}{k} \\\ \end{aligned}$$ Now, we can find the total displacement from the equation for ‘y’ as – $$\begin{aligned} & y=a+2b \\\ & \Rightarrow y=\dfrac{mg}{k}+2(\dfrac{2mg}{k}) \\\ & \therefore y=\dfrac{5mg}{k} \\\ \end{aligned}$$ But we are already given that the total displacement ‘y’ as – $$y=x\times (\dfrac{5mg}{k})$$ From the above two relations we can conclude that – $$\therefore x=1$$ The required value for ‘x’ is 1. This is the required solution. **Note:** The springs when attached to masses undergo extension due to the force due to the mass of the body. This extension is directly proportional to the mass hung on the spring as we have seen in this problem. We have to keep this point in mind while solving these.