Question
Question: All reactions are of \( 1st \) order. At time \( t = t{}_1(t{}_1 > 0) \) \( \dfrac{{[B]}}{{[C]...
All reactions are of 1st order.
At time t=t1(t1>0)
[C][B]=α. Therefore at
Time t =t2 (where t2⩾t1 )
[D][C]=β Which of the following is correct?
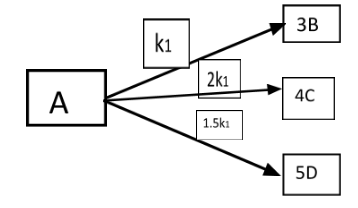
(A) α>β
(B) α=β
(C) αβ=0.4
(D) α+β=0.4
Solution
Let us understand what first order reaction is. And step by step see how we can solve this equation. We first will find the relation between alpha and beta at given concentration and given time.
Complete step by step solution:
A first order reaction is a reaction in which the rate of reaction depends on the concentration of one reactant only. In other words, first order reaction is a chemical reaction where the rate varies based on changes in the concentration of one reactant only. Hence the order all these reaction is equal to 1
k=M(1−n)S−1
All the given reactions are in first order. At the t1 the concentration of [B] and [C] is given by:
[C][B]=α.
All the given reactions are in first order. At the t2 the concentration of [B] and [D] is given by:
[D][C]=β
Let us now find the relation between α and β
At any time the ,
[C][B]=8k13k1=83=α
[D][C]=7.5k18k1=7.58=β
α×β=83×7.58=0.4
Hence the correct answer is option C.
Additional Information:
A differential rate is used to describe a reaction at a molecular level. The differential rate expression for first order reaction is given by:
Rate= −dtd[A]=k[A]1=k[A]
Where,
K is the rate constant
[A] is the concentration of first order reactant
dtd[A] is the change in concentration of the first order reaction A in time interval dt .
Note:
Here are few examples of first order reaction SO2Cl2→Cl2+SO2 , 2NH2O2→O2+4NO2 , 2H2O2→2H2O+O2 . The rate constant is expressed in terms of s1
The units can be determined using the following,
Units of k=M(1−n)S−1 .
