Question

All pulleys are light & smooth, strings are light & inextensible. Consider the case when $\text{M}\to \infty$ (see fig).

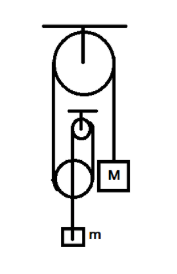
A. Acceleration of $m$ is $g$ upwards.
B. Net force of $m$ is $\dfrac{mg}{3}$ upwards.
C. Tension in the string connecting $M$ is $\dfrac{4mg}{9}$.
D. Tension in the string connecting $m$ is $2mg$.

Answer 1

First we need to mark the tension on the strings attached with masses and pulleys. After that we need to equate the tension on smaller mass, with the force generated from the acceleration due to smaller mass and add it with the force generated from the gravity. The formula of tension due to acceleration and gravity is written as:
For Acceleration:
$T=ma$
For Acceleration due to gravity:
$T=mg$
where $T$ is the tension applied on the strings, $m$ is the mass of the blocks, $a$ is the acceleration and $g$ is the acceleration due to gravity $9.8m{{s}^{-2}}$.

Complete step by step solution:
The tension generated from the pulley and the two masses $m,M$ respectively is given as $T$ as shown below:

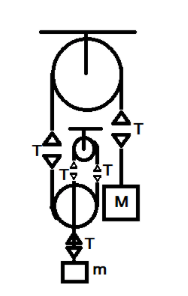
The force generated by the smaller mass $m$, due to its own weight is given as $F=ma$.
The force due to acceleration by gravity, generated by the smaller mass $m$, due to its own weight is given as $F=mg$.
The force generated by the bigger mass $M$, due to its own weight is given as $F=-Ma$. The force is negative as the mass is small compared to the mass $m$ and pulley weight together, hence will move upwards instead of downwards.
The force due to acceleration by gravity, generated by the bigger mass $M$, due to its own weight is given as $F=Mg$.
The relationship between both the masses along with their tension is given as:
$T=mg+ma$ …(1)
$T=Mg-Ma$ …(2)
Placing the values of the tension in the (2) equation to (1) equation. We get the equation between both the masses and acceleration and gravity as:
$\left( \dfrac{M-m}{M+m} \right)g=a$
Now, the mass of the bigger block i.e. $M$ is taken as $\infty$, the final equation will be:
$\Rightarrow \left( \dfrac{\dfrac{M-m}{M}}{\dfrac{M+m}{M}} \right)g=a$ (Dividing both the numerator and denominator with $M$)
$\Rightarrow \left( \dfrac{1-\dfrac{m}{M}}{1+\dfrac{m}{M}} \right)g=a$
With $M$ is taken as $\infty$, the value of $\dfrac{1}{\infty }=0$:
$\Rightarrow \left( \dfrac{1-0}{1+0} \right)g=a$
$\Rightarrow a=g$
Now both the acceleration and gravity are same in this scenario hence, placing the value of acceleration $a$, as $a=g$ in the equations we get:
For mass $m$:
$T=mg+ma$
$\Rightarrow T=mg+mg$
$\Rightarrow T=2mg$ …(3)
For mass $M$:
$T=Mg-Ma$
$\Rightarrow T=Mg-Mg$
$\Rightarrow T=0$ …(4)
Therefore, the tension generated due to mass $m$, is $2mg$.

So, option D is correct

Note: Students may go wrong while finding the force due to acceleration for the bigger mass which is negative as in this case the mass M is moving upwards due to mass and pulley weight on the other side. When force goes in the same direction they add up but with acceleration going in the opposite direction a negative side has been added to the force to separate the force due to acceleration and force due to gravity.