Question

All diodes are ideal. The current flowing in $2\Omega$resistor connected between the diodes ${D_1}$ and ${D_2}$is then:

A) 1A
B) 2A
C) 3A
D) Zero

Answer 1

A diode is a device which allows current to pass in only one direction i.e. it will allow the current to pass in the forward bias only. The resistance for the diode in forward bias is zero and in reverse bias is infinity.

Complete step by step answer:
Here in the second line the diode D4 is reverse bias so there will be no current flowing in it.

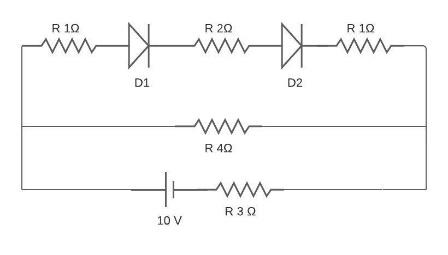
The resistance is in series with each other so, the equivalent resistance will be:
${R_{eq}} = 1\Omega + 2\Omega + 1\Omega$;
The equivalent resistance would be:
$\Rightarrow {R_{eq}} = 4\Omega$;

Now the resistors $4\Omega$ and $4\Omega$ are in parallel with each other. So, the equivalent resistance is:
${R_{eq1}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$ ;
Put in the given values of resistance in the above equation:
$\Rightarrow {R_{eq1}} = \dfrac{{4 \times 4}}{{4 + 4}}$;
$\Rightarrow {R_{eq1}} = \dfrac{{16}}{8} = 2\Omega$;
The resistance$2\Omega$and $3\Omega$are in series with each other:
${R_{eq}} = 2\Omega + 3\Omega$;
$\Rightarrow {R_{eq}} = 5\Omega$;
Now we know the relation between the current, Voltage and Resistor respectively:
${I_{eq}} = \dfrac{V}{{{R_{eq}}}}$ ;
Put in the given values in the above equation and solve:
$\Rightarrow {I_{eq}} = \dfrac{{10}}{5}$;
The equivalent current is:
$\Rightarrow {I_{eq}} = 2A$;
Current in the $2\Omega$ resistor would be 1A.

Option B is correct. The current flowing in $2\Omega$resistor connected between the diodes ${D_1}$ and ${D_2}$is 1A.

Note: Here we need to solve the circuit. First find the equivalent resistance in row 1 which is in series. Then resistance in first row/wire would be in parallel with the resistance in second row/wire. After that the two resistances i.e. $2\Omega$ and $3\Omega$ would be in series with each other. Apply the formula V=IR and solve.