Question

All contact surfaces in the figure are smooth. If the wedge is moved towards right with acceleration ${a_0}$ then the normal force between the wedge and the block will be

A. $mg\cos \theta$
B. $mgsin\theta$
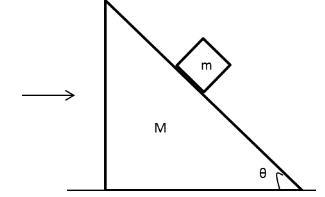
C. $m\left[ {g\sin \theta + {a_0}\cos \theta } \right]$
D. $m\left[ {g\cos \theta + {a_0}\sin \theta } \right]$

Answer 1

Apply Newton’s second law of motion on the block. Draw the horizontal and vertical components of the weight of the block and the acceleration of the block when the wedge is moved toward right with some acceleration. Apply Newton’s second law of motion to the block in the vertical direction.

Formula used:
The expression for Newton’s second law of motion is
${F_{net}} = ma$
Here, ${F_{net}}$ is the net force on the object, $m$ is the mass of the object and $a$ is the acceleration of the object.

Complete step by step answer:
We have given that all the surfaces shown in the given figure are smooth. Hence, we can conclude that there is no static or kinetic frictional force between the block, wedge and horizontal surface.The wedge moves towards right with acceleration ${a_0}$.Draw free body diagram of the block.

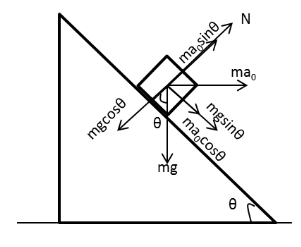
In the above figure, the weight $mg$ of the block with its components is shown. Also the force $m{a_0}$ on the block due to acceleration is also shown. The normal force exerted by the wedge on the block is $N$.
We can determine the normal force exerted by the wedge on the block using Newton’s second law of motion.
Apply Newton’s second law of motion on the block in the vertical direction.
$N - mg\cos \theta = m{a_0}\sin \theta$
Rearrange the above equation for the normal force.
$\Rightarrow N = m{a_0}\sin \theta + mg\cos \theta$
$\Rightarrow N = m\left( {{a_0}\sin \theta + g\cos \theta } \right)$
$\therefore N = m\left[ {g\cos \theta + {a_0}\sin \theta } \right]$
Therefore, the normal force between the wedge and the block will be $m\left[ {g\cos \theta + {a_0}\sin \theta } \right]$.

Hence, the correct option is D.

Note: Newton’s second law of motion is applied to the block only in vertical direction as the required normal force between the block and the wedge is along the vertical direction. The students may take the resultant force due to acceleration $m{a_0}$. Since Newton’s law is applied in vertical direction, the vertical component of force due to acceleration should be considered.