Question
Question: All capacitors used in the below diagram are identical and each has capacitance C. Then, the effecti...
All capacitors used in the below diagram are identical and each has capacitance C. Then, the effective capacitance between the point A and B is
A. 1.5 C
B. 6 C
C. 1 C
D. 3 C
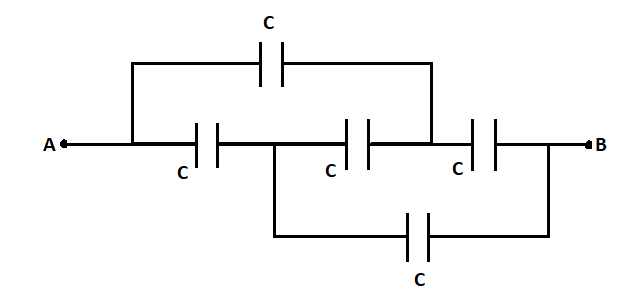
Solution
We can arrange the given figure in a Wheatstone bridge format. It is nothing more than two simple series-parallel arrangements of capacitors connected between two terminals. Find the resultant capacitance of the Wheatstone bridge which will be the effective capacitance between A and B.
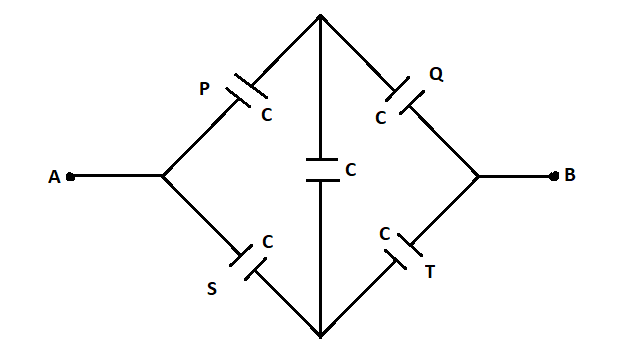
Complete step by step answer:
We are given that a set of 5 capacitors given in the above figure are identical and each have capacitance C.
We have to calculate the effective capacitance between the points A and B.
As we can see, the capacitors form a Wheatstone bridge.
The effective capacitance between A and B is the sum of effective capacitance between P and Q and the effective capacitance between S and T.
CAB=CPQ+CST
Wheatstone bridges can be divided into two halves which have similar capacitance.
∴CPQ=CST
The capacitance CPQ is the reciprocal of the sums of the reciprocal of the capacitances P and Q.
CPQ=CP1+CQ11
The capacitance of the capacitor P is C and capacitance of Q is C.
CPQ=CP1+CQ11 CP=C,CQ=C CPQ=C1+C11 =C21 CPQ=2C
The capacitance CPQ is equal to the capacitance CST
CPQ=CST=2C ⟹CAB=CPQ+CST ⟹CAB=2C+2C ⟹CAB=1C
The effective capacitance between the point A and point B is 1C.
So, the correct answer is “Option C”.
Note:
Capacitance is the ability of a capacitor to store electric charge. Effective Capacitance is the total capacitance existing between any two points in a circuit. When the capacitors are connected in series then the reciprocal of the resultant capacitance will be the sum of the reciprocals of all the capacitances and when the capacitors are connected in parallel then the resultant capacitance will be the sum of all the capacitances; whereas when it comes to resistors it is vice versa. When the resistors are connected in parallel then the reciprocal of the resultant resistance will be the sum of the reciprocals of all the resistances and when the resistors are connected in parallel then the resultant resistance will be the sum of all the resistances. Do not confuse the series and parallel configurations among resistors and capacitors.
