Question

Airplanes $A$ and $B$ are flying with constant velocity in the same vertical plane at angles ${30^ \circ }$ and ${60^ \circ }$ with respect to the horizontal respectively as shown in the figure. The speed of $A$ is $100\sqrt 3 m{s^{ - 1}}$ . At time $t = 0s$ , an observer in $A$ finds $B$ at a distance of $500m$ . This observer sees $B$ moving with a constant velocity perpendicular to the line of motion of $A$ . If at $t = {t_0}$ , $A$ just escapes being hit by $B$ , ${t_0}$ in seconds is:

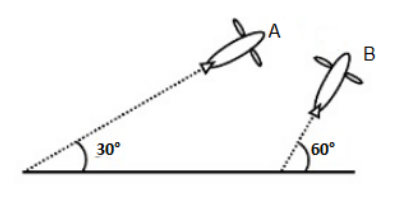
\left( A \right)5 \\\ \left( B \right)7 \\\ \left( C \right)6 \\\ \left( D \right)8 \\\

Answer 1

Hint : In this question, we are going to first divide the two velocities into horizontal and vertical components. By equating the components, the velocity ${V_B}$ is calculated. From ${V_B}$ , the time for the escape can be calculated from the distance given and the vertical component of the velocity ${V_B}$ .
The horizontal and the vertical components of a velocity $V$ with projection angle $\theta$ are $V\cos \theta$ and $V\sin \theta$ respectively.
The time taken for $B$ is
${T_0} = \dfrac{{distance}}{{vertical{\text{ }}component{\text{ }}of speed{\text{ }}of{\text{ }}B}}$

Complete Step By Step Answer:
In the given figure, we can see that the velocities ${V_A}$ and ${V_B}$ can be split into its vertical and horizontal components.

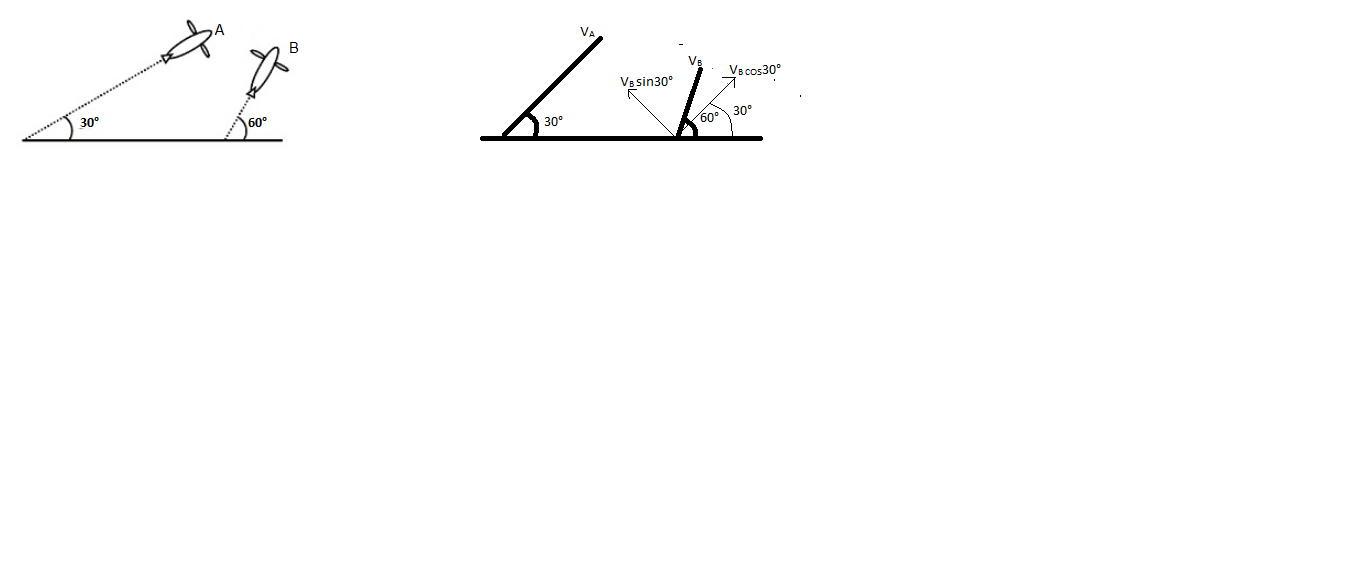
The components of the velocities can be related as
${V_A} = {V_B}\cos {30^ \circ }$
Here, if we put the values of the velocity ${V_A}$ and $\cos {30^ \circ }$ , we get, the value of ${V_B}$ as:
$100\sqrt 3 = {V_B} \times \dfrac{{\sqrt 3 }}{2}$
On solving this, we get
${V_B} = 200m{s^{ - 1}}$
Here, we are given that the distance between the two planes is $500m$ and also that the observer sees that the motion of $B$ moving with a constant velocity perpendicular to the line of motion of $A$ thus, the time $t = {t_0}$ at which $A$ just escapes being hit by $B$ , is
${T_0} = \dfrac{{distance}}{{vertical{\text{ }}component{\text{ }}of speed{\text{ }}of{\text{ }}B}}$
Putting the values, we get
{T_0} = \dfrac{{500}}{{{V_B}\sin {{30}^ \circ }}} = \dfrac{{500}}{{200 \times \dfrac{1}{2}}} \\\ \Rightarrow {T_0} = 5s \\\
Hence, option $\left( A \right)5$ is the correct answer.

Note :
In the question, we are given that the distance along the line of motion is $500m$ , along this direction, the velocity that is prevalent is the vertical component of the velocity along the angle ${30^ \circ }$ . Where the horizontal component of the velocity ${V_B}$ is equal to the speed of the airplane $A$ .