Question

Air speed of an airplane is $400km{{h}^{-1}}$. The wind is blowing at $200km{{h}^{-1}}$ towards east direction. In what direction should the pilot try to fly the plane so as to move exactly towards the north east.

Answer 1

The flow of the wind will affect the motion of the plane. The resultant velocity of the plane will be equal to the vector sum of the airspeed of the plane and the velocity of the wind. Draw a vector diagram and find the angle that the pilot should make for the required condition.

Complete step by step answer:
When an airplane flies in presence of a wind, the speed and direction of the wind affects the motion of the plane. The wind may either assist the motion of the plane or oppose the motion of the plane depending upon the speed and direction of the wind.In this case, the wind is blowing with a speed of $200km{{h}^{-1}}$ towards east. This will increase the speed of the plane by $200km{{h}^{-1}}$ towards east. Let the initial direction of the plane be making an angle $\theta$ with horizontal and the plane will move with a speed of $400km{{h}^{-1}}$. Due to this the resultant velocity of the plane will be equal to the vector sum of the airspeed of the plane and the velocity of the wind, as shown in the figure.

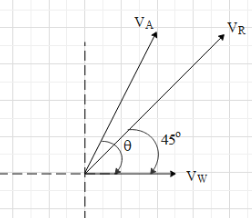
Here, ${{V}_{A}}$ is the airspeed of the plane, ${{V}_{W}}$ is the velocity of the wind and ${{V}_{R}}$ is the resultant velocity of the plane.

Since ${{V}_{R}}$ is resultant of ${{V}_{A}}$ and ${{V}_{W}}$, the vertical component of the ${{V}_{R}}$ is equal to sum of the vertical components of the ${{V}_{A}}$ and ${{V}_{W}}$.
i.e. $\dfrac{{{V}_{R}}}{\sqrt{2}}={{V}_{A}}\sin \theta$ .…. (i)
And the horizontal component of ${{V}_{R}}$ is equal to sum of the horizontal components of the ${{V}_{A}}$ and ${{V}_{W}}$.
i.e. $\dfrac{{{V}_{R}}}{\sqrt{2}}={{V}_{A}}\cos \theta +{{V}_{W}}$ ….. (ii).
Now, equate (i) and (ii).
$\Rightarrow {{V}_{A}}\sin \theta ={{V}_{A}}\cos \theta +{{V}_{W}}$
$\Rightarrow {{V}_{A}}\sin \theta -{{V}_{A}}\cos \theta ={{V}_{W}}$
Substitute ${{V}_{A}}=400km{{h}^{-1}}$ and ${{V}_{W}}=200km{{h}^{-1}}$.
$\Rightarrow 400\sin \theta -400\cos \theta =200$
$\Rightarrow \sin \theta -\cos \theta =\dfrac{1}{2}$
Divide the equation by $\cos {{45}^{\circ }}=\dfrac{1}{\sqrt{2}}$.
$\Rightarrow \sin \theta \cos {{45}^{\circ }}-\cos \theta \cos {{45}^{\circ }}=\dfrac{1}{2\sqrt{2}}$
But from trigonometry we know that,
$\sin \theta \cos {{45}^{\circ }}-\cos \theta \cos {{45}^{\circ }}=\sin (\theta -{{45}^{\circ }})$.
Then,
$\Rightarrow \sin (\theta -{{45}^{\circ }})=\dfrac{1}{2\sqrt{2}}$
$\Rightarrow \theta -{{45}^{\circ }}={{\sin }^{-1}}\dfrac{1}{2\sqrt{2}}$
$\Rightarrow \theta -{{45}^{\circ }}={{20.7}^{\circ }}$
$\therefore \theta ={{20.7}^{\circ }}+{{45}^{\circ }}={{65.7}^{\circ }}$

Therefore, in order to fly the plane towards north-east, the pilot must try to fly the plane in the direction that makes an angle of ${{65.7}^{\circ }}$ with a positive x-axis.

Note: In order to solve direction problems students may be confused in direction. So always remember below chart

And always assume all distances to be along straight lines and between specified points each main direction changes north to west /east, it will be $90{}^\circ$change but the change between north and north east is only $45{}^\circ$.