Question

For reaction: A → 3B, takes place as per first order kinetics, the time in which the concentration of reactant and product, become equal is (nearest integer)

(Given: k = 4.6×$10^{-2}$ $min^{-1}$, log 3 = 0.48, log 2 = 0.3)

Answer 1

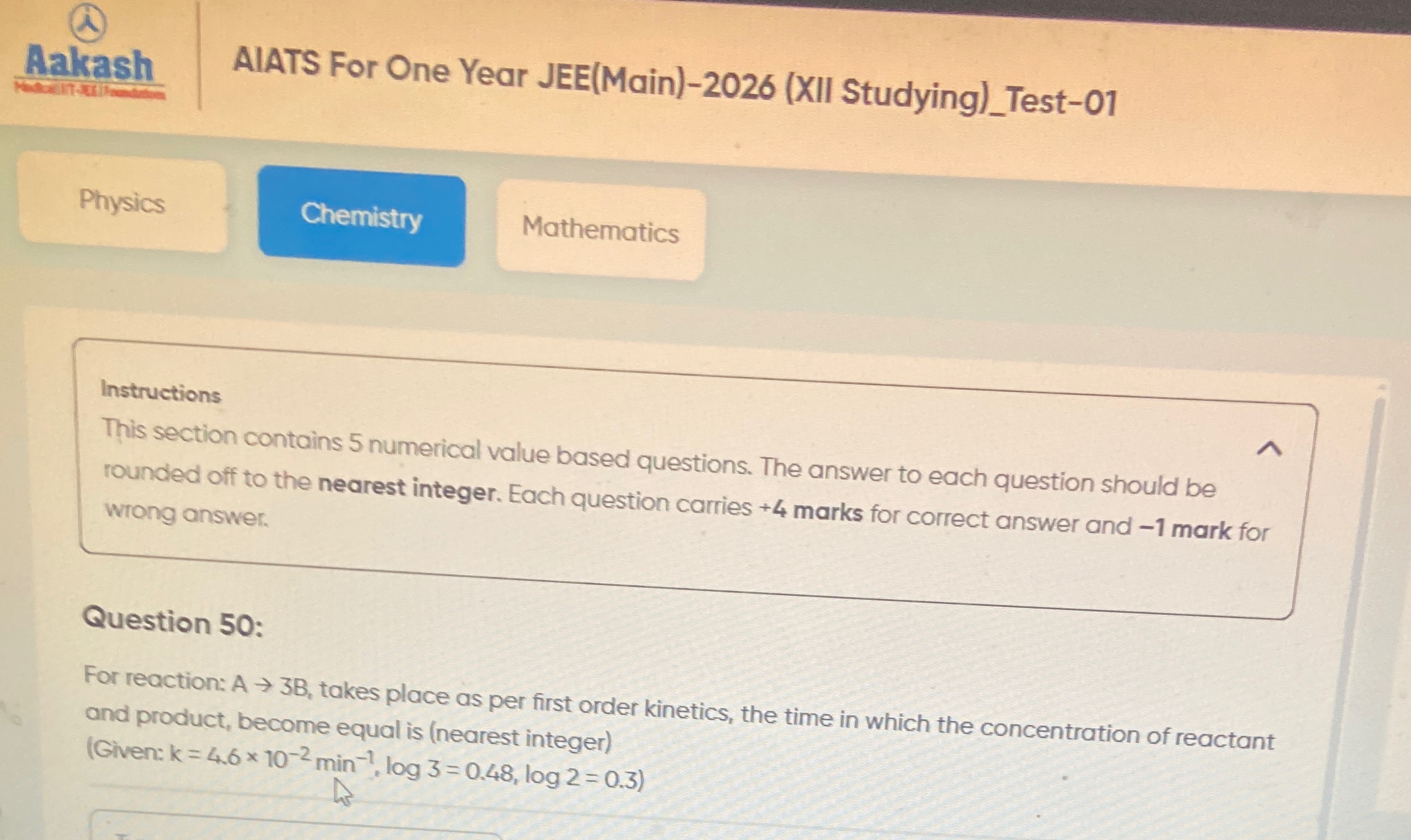
6

Answer 2

The problem asks for the time when the concentration of the reactant (A) and the product (B) become equal for a first-order reaction A → 3B.

1. Define initial and final concentrations: Let the initial concentration of reactant A be $[A]_0$.
At time $t$, let $x$ be the concentration of A that has reacted.
According to the stoichiometry of the reaction A → 3B:
If $x$ moles of A react, then $3x$ moles of B are formed.

The concentration of reactant A at time $t$ will be:
$[A]_t = [A]_0 - x$

The concentration of product B at time $t$ will be:
$[B]_t = 3x$

2. Set up the condition for equal concentrations: We are given that at time $t$, the concentration of reactant and product become equal:
$[A]_t = [B]_t$
Substitute the expressions for $[A]_t$ and $[B]_t$:
$[A]_0 - x = 3x$
$[A]_0 = 4x$
From this, we can express $x$ in terms of $[A]_0$:
$x = \frac{[A]_0}{4}$

Now, find the concentration of A remaining at time $t$, $[A]_t$, in terms of $[A]_0$:
$[A]_t = [A]_0 - x = [A]_0 - \frac{[A]_0}{4} = \frac{3[A]_0}{4}$

3. Apply the integrated rate law for a first-order reaction: For a first-order reaction, the integrated rate law is:
$t = \frac{1}{k} \ln\left(\frac{[A]_0}{[A]_t}\right)$

Substitute the expression for $[A]_t$ into the equation:
$t = \frac{1}{k} \ln\left(\frac{[A]_0}{3[A]_0/4}\right)$
$t = \frac{1}{k} \ln\left(\frac{4}{3}\right)$

4. Substitute the given values and calculate $t$: Given:
Rate constant, $k = 4.6 \times 10^{-2} \text{ min}^{-1}$
$\log 3 = 0.48$
$\log 2 = 0.3$

We need to convert the natural logarithm ($\ln$) to base-10 logarithm ($\log$):
$\ln x = 2.303 \log x$

So, the equation for $t$ becomes:
$t = \frac{2.303}{k} \log\left(\frac{4}{3}\right)$
$t = \frac{2.303}{k} (\log 4 - \log 3)$
Since $\log 4 = \log (2^2) = 2 \log 2$:
$t = \frac{2.303}{k} (2 \log 2 - \log 3)$

Now, substitute the numerical values:
$t = \frac{2.303}{4.6 \times 10^{-2}} (2 \times 0.3 - 0.48)$
$t = \frac{2.303}{0.046} (0.6 - 0.48)$
$t = \frac{2.303}{0.046} (0.12)$
$t = 50.065217 \times 0.12$
$t = 6.007826 \text{ min}$

5. Round to the nearest integer: Rounding $6.007826$ to the nearest integer gives $6$.

The final answer is $\boxed{6}$.