Question

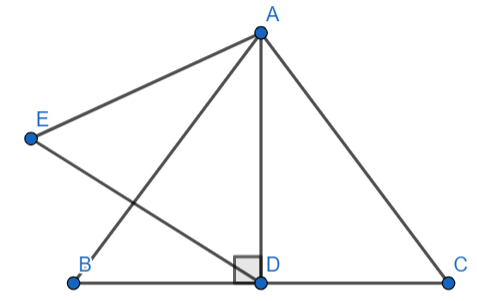
AD is an altitude of an equilateral $\Delta ABC$ . On AD as base, another equilateral $\Delta ADE$ is constructed. Prove that:
$\dfrac{ar\left( \Delta ADE \right)}{ar\left( \Delta ABC \right)}=\dfrac{3}{4}$

Answer 1

Hint: Assume that each side of the equilateral $\Delta ABC$ is x units. Use the formula, $Area=\dfrac{\sqrt{3}}{4}{{\left( side \right)}^{2}}$ and calculate the area of $\Delta ABC$ . We know that the length of the perpendicular of an equilateral triangle is $\dfrac{\sqrt{3}}{2}side$ . Now, get the length of the perpendicular of $\Delta ABC$ . It is given that the length of the base of $\Delta ADE$ is equal to the length of the perpendicular of $\Delta ABC$ . So, the length of each side of $\Delta ADE$ is equal to the length of the perpendicular of $\Delta ABC$ . Now, use the formula, $Area=\dfrac{\sqrt{3}}{4}{{\left( side \right)}^{2}}$ and calculate the area of $\Delta ADE$ . Then, calculate $\dfrac{ar\left( \Delta ADE \right)}{ar\left( \Delta ABC \right)}$.

Complete step-by-step answer:
First of all, let us assume that each side of the equilateral $\Delta ABC$ is x units.
The length of each side of $\Delta ABC$ = x ………………………………..(1)

We know the formula of area of equilateral triangle, $Area=\dfrac{\sqrt{3}}{4}{{\left( side \right)}^{2}}$ ………………………………..(2)
From equation (1), we have the length of each side of $\Delta ABC$ .
Now, putting the value of length of each side equal to x in equation (2), we get
The area of $\Delta ABC$ = $\dfrac{\sqrt{3}}{4}{{\left( x \right)}^{2}}=\dfrac{\sqrt{3}{{x}^{2}}}{4}$ …………………………….(3)
We know that the length of the perpendicular of an equilateral triangle is $\dfrac{\sqrt{3}}{2}side$ .
Since the side if $\Delta ABC$ is x units so, the length of the perpendicular of $\Delta ABC$ is $\dfrac{\sqrt{3}}{2}x$ ………………………………(4)
It is given that the length of the base of $\Delta ADE$ is equal to the length of the perpendicular of $\Delta ABC$ .
From equation (4), we have the length of the perpendicular of $\Delta ABC$ .
The length of the base of $\Delta ADE$ = $\dfrac{\sqrt{3}}{2}x$ ……………………………………(5)
As $\Delta ADE$ is an equilateral triangle so, the length of each side is same as the length of the base of $\Delta ADE$ .
The length of each side of $\Delta ADE$ = $\dfrac{\sqrt{3}}{2}x$ ………………………………….(6)
From equation (6), we have the length of each side of $\Delta ADE$ .
Now, putting the value of length of each side equal to x in equation (2), we get
The area of $\Delta ADE$ = $\dfrac{\sqrt{3}}{4}{{\left( \dfrac{\sqrt{3}}{2}x \right)}^{2}}=\dfrac{3}{4}\times \dfrac{\sqrt{3}{{x}^{2}}}{4}$ …………………………….(7)
Now, from equation (3) and equation (7), we have the area of $\Delta ABC$ and $\Delta ADE$ .
$\dfrac{ar\left( \Delta ADE \right)}{ar\left( \Delta ABC \right)}=\dfrac{\dfrac{3}{4}\times \dfrac{\sqrt{3}{{x}^{2}}}{4}}{\dfrac{\sqrt{3}{{x}^{2}}}{4}}=\dfrac{3}{4}$
LHS = RHS.
Hence, proved.

Note: While solving this question, one might get confused and can think why the length of the perpendicular of an equilateral triangle is $\dfrac{\sqrt{3}}{2}side$ .
Let us assume an equilateral triangle whose length of each side is x units.

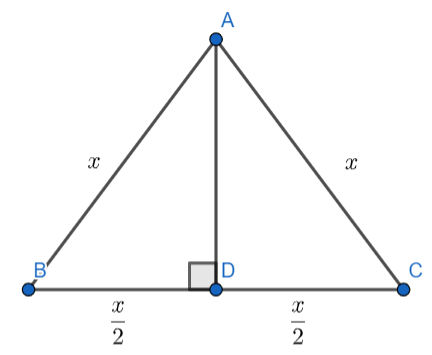
In the $\Delta ABC$ , AD is perpendicular to the base BC.
We know the property that the perpendicular bisects the base in an equilateral triangle.
So, the perpendicular AD bisects the base BC,
Therefore, $BD=CD$ …………………………….(1)
Since the length of each side of $\Delta ABC$ is equal to x so, the length of the base BC is also x.
BC = x …………………………………(2)
From the figure, we can see that
$\Rightarrow BC=BD+CD$
Now, from equation (1) and equation (2), we get

& \Rightarrow x=BD+BD \\\ & \Rightarrow x=2BD \\\ \end{aligned}$$ $$\Rightarrow \dfrac{x}{2}=BD$$ …………………………………(3) Now, in $$\Delta ADB$$ , we have $$\angle ADB=90{}^\circ $$ …………………………………(4) Hypotenuse = AB = x (side of each side of $$\Delta ABC$$ is equal to x) …………………………………(5) Base = BD = $$\dfrac{x}{2}$$ ……………………………….(6) Perpendicular = AD ………………………………….(7) Since $$\Delta ADB$$ is an equilateral triangle, so we can apply the Pythagoras theorem here. $${{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}$$ ………………………..(8) Now, from equation (4), equation (5), equation (6), equation (7), and equation (8), we get $$\begin{aligned} & \Rightarrow {{\left( x \right)}^{2}}={{\left( AD \right)}^{2}}+{{\left( \dfrac{x}{2} \right)}^{2}} \\\ & \Rightarrow {{x}^{2}}=A{{D}^{2}}+\dfrac{{{x}^{2}}}{4} \\\ & \Rightarrow {{x}^{2}}-\dfrac{{{x}^{2}}}{4}=A{{D}^{2}} \\\ & \Rightarrow \dfrac{4{{x}^{2}}-{{x}^{2}}}{4}=A{{D}^{2}} \\\ & \Rightarrow \dfrac{3{{x}^{2}}}{4}=A{{D}^{2}} \\\ \end{aligned}$$ $$\Rightarrow \dfrac{\sqrt{3}x}{2}=AD$$ Here, AD is the length of the perpendicular and x is the length of the side of equilateral $$\Delta ABC$$ . Therefore, the length of the perpendicular of an equilateral triangle is $$\dfrac{\sqrt{3}}{2}side$$ .