Solveeit Logo
Login

Question

Question: According to this example, the COM of a composite body (having two or more basic shapes, combined) l...

According to this example, the COM of a composite body (having two or more basic shapes, combined) lies in a heavier part.

A) Yes.
B) No.
C) Can’t say.
D) None of these.

Explanation

Solution

The centre of mass is defined as the position on the body or system of the body where all the mass is assumed to be distributed. The centre of mass is very important to bear with

Formula used: The formula for calculating the centre of mass is given by,
⇒r⃗com=∑mi(r⃗com)i∑mi\Rightarrow {\vec r_{com}} = \dfrac{{\sum {{m_i}} {{\left( {{{\vec r}_{com}}} \right)}_i}}}{{\sum {{m_i}} }}
Where mi{m_i} is the mass of the body and (r⃗com)i{\left( {{{\vec r}_{com}}} \right)_i} is the position of the object.

Step by step solution:
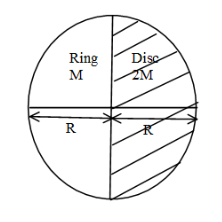
It is asked in the problem that the centre of mass of a composite body does always lie in the heavier part of the composite body.
For solving this we will have some assumptions:
-We will assume that mass is uniformly distributed in both the parts of the composite body.
-There is no cavity present in the body.
The center of mass of the ring will be at distance 2Rπ\dfrac{{2R}}{\pi } from the y-axis and the center of mass of the disc will be at 4R3π\dfrac{{4R}}{{3\pi }} from the y-axis.
Now let us calculate the center of mass of the composite body.
The formula for calculating the centre of mass is given by,
⇒r⃗com=∑mi(r⃗com)i∑mi\Rightarrow {\vec r_{com}} = \dfrac{{\sum {{m_i}} {{\left( {{{\vec r}_{com}}} \right)}_i}}}{{\sum {{m_i}} }}
Where mi{m_i} is the mass of the body and (r⃗com)i{\left( {{{\vec r}_{com}}} \right)_i}is the position of the object from the x-axis or y-axis.
⇒r⃗com=∑mi(r⃗com)i∑mi\Rightarrow {\vec r_{com}} = \dfrac{{\sum {{m_i}} {{\left( {{{\vec r}_{com}}} \right)}_i}}}{{\sum {{m_i}} }}
⇒r⃗com=M(r⃗com)ring+2M(r⃗com)disc2M+M\Rightarrow {\vec r_{com}} = \dfrac{{M{{\left( {{{\vec r}_{com}}} \right)}_{ring}} + 2M{{\left( {{{\vec r}_{com}}} \right)}_{disc}}}}{{2M + M}}
⇒r⃗com=[M×−2Rπ+2M×4R3π3M]i^\Rightarrow {\vec r_{com}} = \left[ {\dfrac{{M \times - \dfrac{{2R}}{\pi } + 2M \times \dfrac{{4R}}{{3\pi }}}}{{3M}}} \right]\hat i
⇒r⃗com=2R9πi^\Rightarrow {\vec r_{com}} = \dfrac{{2R}}{{9\pi }}\hat i
Here we get that the r⃗com{\vec r_{com}} lies on the heavier side of the composite body, so the given statement in the problem is true.

The correct option for this problem is option A.

Note: The centre of mass concept is very important for the calculation of the many problems of large bodies. If the large bodies are considered as point mass then the calculation becomes very easy and more accurate.