Question

According to the law of reflection:
(A) $\dfrac{i}{r} = cons\tan t$
(B) $\sin {\text{i/sin }}r = {\text{constant}}$
(C) $i + r = cons\tan t$
(D) $i = r$

Answer 1

When a ray of light reflects from the surface after the incidence, then the angle of incidence is equal to the angle of reflection.Reflection of light is the change in the direction of the wavefront at an interface between two different media so that the wavefront returns into the medium from which it is originated. The reflection of light is either like a mirror or diffusive where the image does not form.

Complete step by step answer:
There are basically three laws of reflections where,
The first law of reflection states that the incident ray, the reflected ray, and the normal to the reflected surface at the point of the incidence lie in the same plane.

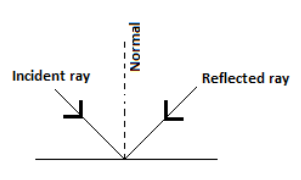
The second law of reflection states that the angle made by the incidence ray from the normal is equal to the angle made by the reflected ray from normal.

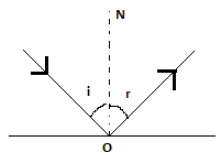
Where I is the angle of incidence, and r is the angle of reflection.
The third law of reflection says that the incidence ray and the reflected ray are on the opposite side of the normal.

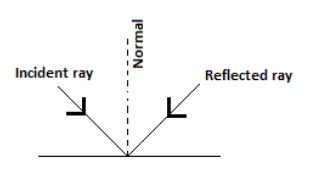
The law of reflection formula is given as $i = r$, where $i$is the angle incidence and $r$is the angle of reflection

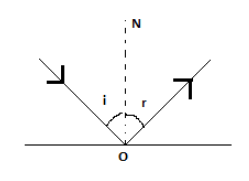
Hence, option D is correct.

Note: Student must note that the normal is a line which is drawn perpendicular to a reflecting surface. The normal ray is incident at 90 degrees to the reflecting surface.