Question
Question: According to the Geiger-Nuttall Law the curve between \(\log \lambda \) and \(\log R\) will be A. ...
According to the Geiger-Nuttall Law the curve between logλ and logR will be
A. 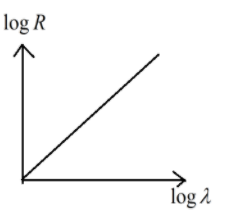
B. 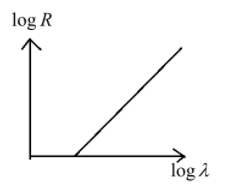
C. 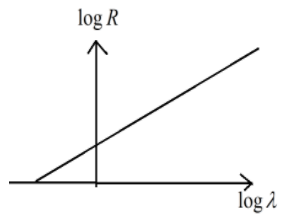
D.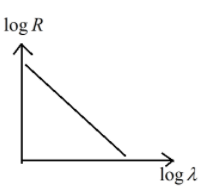
Solution
We need to understand the Geiger–Marsden experiment in order to solve this. Geiger and Marsden did a large number of experiments where they observed a beam of alpha particles at a thin foil of a metal piece and measured the pattern of scattering by using a fluorescent screen.
Complete answer:
Geiger and Marsden observed alpha particles are getting reflected in the metal foil in all directions.
Those particles had encountered an electrostatic force far greater than Thomson's model suggested they would, which is nothing but the atom's positive charge was concentrated in a much lesser volume than Thomson imagined.
When Geiger and Marsden shot alpha particles at their metal foils, they found that only a lesser amount of the alpha particles were deflected by more than 90°. Most of them have gone straight through the foil. This says that those tiny spheres of intense positive charge were separated by the empty space. Most particles were passed through the empty space and had no deviation.
So the relation obtained is as follows
logλ=mlogR+D
Rearrange the above equation
logλ−D=mlogR
mlogR=logλ−D
logR=m1logλ−mD
This represents the linear equation of the form y=mx−c
Hence option (B) is the correct answer.
Note:
Rutherford thus rejected Thomson's model of the atom, and instead he proposed a model where the atom consisted of most of the empty space, with all its positive charge concentrated in its center in less volume, surrounded by a cloud of electrons.
