Question

According to Kepler's third law the relation between orbital period (T) of a planet around the sun and its mean distance (r) from the sun is
A. ${r^3}/{T^3} = {\text{constant}}$
B. ${r^2}/{T^3} = {\text{constant}}$
C. $r/{T^2} = {\text{constant}}$
D. ${r^3}/{T^2} = {\text{constant}}$
E. ${r^3}/T = {\text{constant}}$

Answer 1

The basic forces of nature are gravitational force, electrostatic force, strong nuclear force, weak nuclear force. gravitational force is the long-range force and weakest of the forces. It also acts between the sun and planets revolving around the sun. This gravitational force provides the force required for the curvilinear motion of the planets.

Complete step-by-step solution:
Gravitational force acts between any two masses in the universe. But since the gravitational constant we multiply to get the force is very small the force between two normal masses on earth cannot be experienced.
But if the masses are very huge like planets and the sun then the gravitational force between them is too high.
Kepler has stated three laws regarding the planets.
The first law states that the planets revolve around the sun in elliptical orbits by having the sun at one of the foci

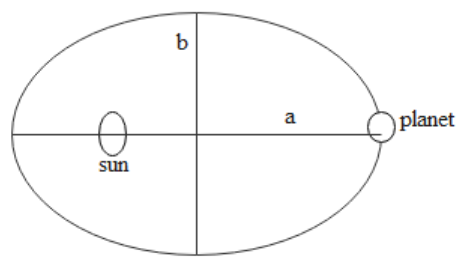
‘a’ in the ellipse is the length of the semi-major axis while ‘b’ is the length of the semi-minor axis.
The second law states that the areal velocity of rotation of planets will be constant.
The third law tells us the relation between the time period of revolution of the planet(T) and the mean distance between the planet and sun(r). The time period of rotation is the ratio of circumference to the velocity of rotation. In the case of elliptical orbits ‘r’ will be the semi-major axis of the ellipse.
Let us derive Kepler’s third law. Let the centripetal force is denoted by ${F_C}$ and the gravitational force of attraction between the planet of mass ‘m’ and sun of mass ‘M’ be ${F_G}$. Let the velocity of rotation be ‘v’. G is the gravitational constant.
The centripetal force is required for the rotation of the planet around the sun and it is provided by that gravitational force of attraction. So
\eqalign{ & {F_C} = {F_G} \cr & \Rightarrow \dfrac{{m{v^2}}}{r} = \dfrac{{GmM}}{{{r^2}}} \cr & \Rightarrow v = \sqrt {\dfrac{{GM}}{r}} \cr & \Rightarrow T = \dfrac{{2\pi r}}{v} \cr & \Rightarrow T = \dfrac{{2\pi r}}{{\sqrt {\dfrac{{GM}}{r}} }} \cr & \Rightarrow T\propto {r^{\dfrac{3}{2}}} \cr & \Rightarrow {T^2}\propto {r^3} \cr}
The relation will be
\eqalign{ & {T^2}\propto {r^3} \cr & \Rightarrow \dfrac{{T^2}}{{r^3}} = {\text{constant}} \cr & \Rightarrow \dfrac{{r^3}}{{T^2}} = {\text{constant}} \cr}
In case of elliptical orbits, ‘r’ will be the semi-major axis of the ellipse. That means $r = a$ for elliptical orbits
Hence option D will be the answer.

Note: The main reason why it’s the mean distance from the sun but not just distance is because the planets revolve in elliptical orbits. That means the distance between the sun and the planet is not constant; it will be varying. If it is a circular orbit then radial distance will be constant but since it is elliptical orbit we talk terms of mean distance only as ellipse major and minor axes.