Question
Question: Acceleration versus velocity graph of a particle moving in a straight line starting from rest is as ...
Acceleration versus velocity graph of a particle moving in a straight line starting from rest is as shown in figure. The corresponding velocity time graph would be:
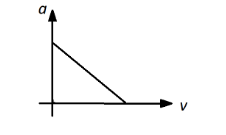
(A)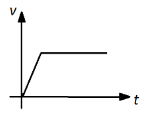
(B)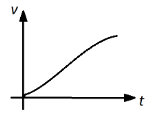
(C) 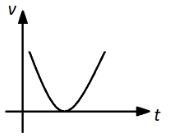
(D) 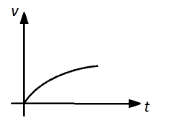
Solution
The above problem is based on the graphical analysis of the physical quantities in kinematics. The slope of the velocity time graph gives the acceleration of the particle and slope of the displacement time graph gives velocity of the particle. The above problem can be solved by finding the equation for the acceleration versus velocity graph of the motion of the particle.
Complete step by step answer:
The general expression for the given graph can be given as:
y=cx
The horizontal axis shows the velocity of the particle and vertical axis shows the acceleration of the particle, so the equation of motion of the particle can be written as:
a=mv......(1)
Here, m is the slope of the acceleration versus time graph, a is the acceleration and v is the velocity of the particle.
The acceleration of the particle is given as:
a=dtdv
Substitute the value of acceleration in the expression (1) .
dtdv=mv
⇒vdv=mdt......(2)
Integrate the expression (2) to find the equation of velocity-time graph of the particle.
∫vdv=∫mdt
⇒lnv=mt+k
∴v=emt+k......(3)
Here k is the constant of integration.
Above expression (3) shows that the velocity of the particle varies exponentially with the time, so the velocity-time graph of the particle will be an exponential graph.
Thus, the velocity-time graph of the particle will be an exponential graph and the option (D) is the correct answer.
Note: Always solve the problems of the graphical analysis of the particle by using the differential form of the velocity and acceleration. Any type of the graph can be found by the given graph by the above mentioned method.
