Question

Acceleration of a particle of mass 2 kg, moving in space is given as $\vec{a} = (-9x\hat{i} - 16y\hat{j})m/s^2$. Initially the particle is at origin and its velocity is $\vec{v_0} = (3\hat{i} + 4\hat{j} + \frac{1}{\sqrt{2}}\hat{k})m/s$. At time $t = \frac{\pi}{12}sec$, the kinetic energy of the particle is ______ Joule.

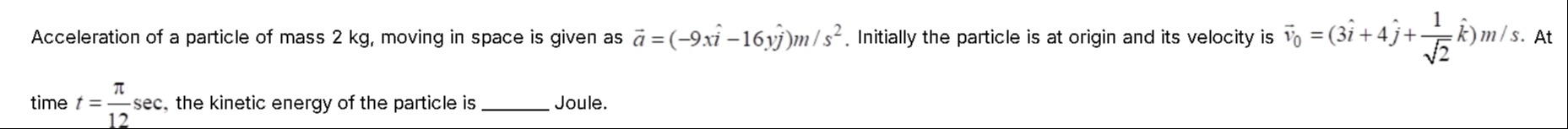
Answer 1

9 Joule

Answer 2

The particle has mass $m = 2$ kg and an acceleration given by

$$\vec{a} = -9x\,\hat{i} - 16y\,\hat{j}.$$

This implies:

• In the $x$-direction:

$$\frac{d^2x}{dt^2} = -9x,$$

with $x(0)=0$ and $v_x(0)=3$. The solution is simple harmonic motion:

$$x(t) = \frac{v_x(0)}{3}\sin(3t) = \sin(3t),$$

so the velocity is

$$v_x(t)=3\cos(3t).$$

• In the $y$-direction:

$$\frac{d^2y}{dt^2} = -16y,$$

with $y(0)=0$ and $v_y(0)=4$. Thus,

$$y(t) = \frac{v_y(0)}{4}\sin(4t) = \sin(4t),$$

and

$$v_y(t)=4\cos(4t).$$

• In the $z$-direction, there is no acceleration so:

$$v_z(t) = \frac{1}{\sqrt{2}} \quad (\text{constant}).$$

At $t = \frac{\pi}{12}$ seconds:

$$v_x = 3\cos\left(3\cdot\frac{\pi}{12}\right)=3\cos\left(\frac{\pi}{4}\right)= 3\cdot \frac{\sqrt{2}}{2} = \frac{3\sqrt{2}}{2},$$ $$v_y = 4\cos\left(4\cdot\frac{\pi}{12}\right)=4\cos\left(\frac{\pi}{3}\right)= 4\cdot \frac{1}{2}= 2,$$ $$v_z = \frac{1}{\sqrt{2}}.$$

The kinetic energy (KE) is given by:

$$\text{KE}=\frac{1}{2} m (v_x^2+v_y^2+v_z^2).$$

Compute each velocity squared:

$$v_x^2=\left(\frac{3\sqrt{2}}{2}\right)^2=\frac{18}{4}=\frac{9}{2},$$ $$v_y^2=2^2=4,$$ $$v_z^2=\left(\frac{1}{\sqrt{2}}\right)^2=\frac{1}{2}.$$

Thus,

$$v_x^2+v_y^2+v_z^2 = \frac{9}{2}+4+\frac{1}{2} = \frac{9+1}{2}+4= \frac{10}{2} +4 =5+4=9.$$

Now,

$$\text{KE}=\frac{1}{2}\times2\times 9 =9\text{ Joule}.$$