Question

ACCELERATION DUE TO GRAVITY BELOW AND ABOVE THE SURFACE OF THE EARTH. Which of the following statements given is correct?
A. Acceleration due to gravity will increase with increasing altitude.
B. Acceleration due to gravity will increase with increasing depth
C. Acceleration due to gravity will increase with increasing latitude
D. Acceleration due to gravity is given as not dependent on the mass of the earth.

Answer 1

Consider each and every sentence or the statements given in the question. Prove every statement in the options and then find out the answer. The acceleration due to gravity decreases with increasing amplitude, increasing depth, decreasing latitude and depends on mass of the earth.

Complete step by step answer:
Let us discuss each and every statement given in the question.
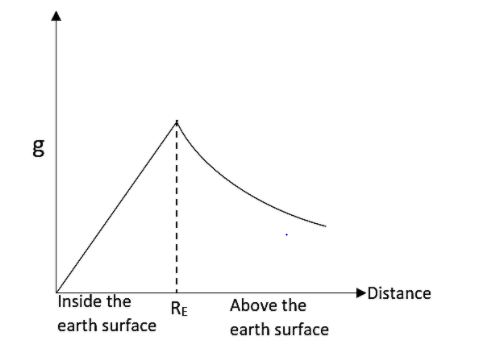
A. The acceleration due to gravity above the surface of earth is given by the equation,
${{g}_{h}}=\dfrac{g{{R}_{E}}^{2}}{{{\left( {{R}_{E}}+h \right)}^{2}}}$
Where $g$ be the acceleration due to gravity, ${{R}_{E}}$ be the radius of the earth, $h$ be the height above the surface of the earth.
From this equation, we can see that, as the height increases the acceleration due to gravity is decreasing. Therefore the statement is found to be incorrect.
B. the acceleration due to gravity below the surface of earth or at a depth is given by the equation,
${{g}_{d}}=g\left( 1-\dfrac{d}{{{R}_{E}}} \right)$
Where $d$ be the depth from the surface. When we look into this equation, we can see that as depth increases, the acceleration due to gravity is decreasing. Therefore the statement is incorrect.
C. the acceleration due to gravity at a given latitude is given as the equation,
${{g}_{\lambda }}=g-{{R}_{E}}{{\omega }^{2}}{{\cos }^{2}}\lambda$
Where $\lambda$ be the latitude and $\omega$ be the angular speed of rotation of earth.
From this equation we can see that as the latitude increases, the cosine terms will get decreased, therefore the acceleration due to gravity will get increased. Therefore this statement is found to be correct.
D. acceleration of a mass place on the surface of earth is given as,
$g=\dfrac{G{{M}_{E}}}{{{R}_{E}}^{2}}$
From this we can see that the acceleration due to gravity is independent of the mass of the object, but depends on the mass of the earth. Therefore this statement is also incorrect.

Therefore the answer is given as option C.

Note:
Acceleration due to gravity is the acceleration obtained by a body in the presence of gravitational force. This is the free fall acceleration is space. This is a vector quantity also, depending on both magnitude and direction of the quantity.