Question

$ACB$ is a right-angled glass prism with refractive index $1.5$. Angle $A$, $B$, $C$ are ${60^ \circ }$,${30^ \circ }$and ${90^ \circ }$ respectively. A thin layer of liquid is on the $AB$. For a ray of light which is incident normally on $AC$ to; be totally reflected at $AB$, the refractive index of the liquid on $AB$ should be;
(A) $1.5$
(B) $1.4$
(C) $1.3$
(D) $1.2$

Answer 1

The above given problem can be solved using the formula that was formulated from Snell's law of refraction with the angle of incident ray and the angle of refractive ray that comes out of the right-angled glass prism.

Formulae Used:
According to Snell’s law of refraction the refractive index of liquid is given by:
$\dfrac{{\sin \,i}}{{\sin \,r}} = \dfrac{\mu }{{{\mu _1}}}$
Where, $\sin \,i$ denotes the angle of incident ray, $\sin \,r$ denotes the angle of refractive ray, $\mu$ denotes the refractive index of the liquid, ${\mu _1}$ denotes the refractive index of the right-angled glass prism.

Complete step-by-step solution:

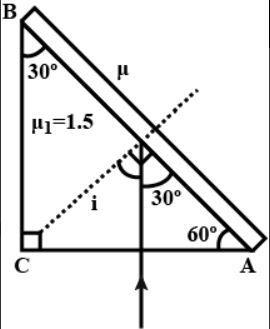
The data given in the problem is;
The refractive index of the right-angled glass prism, ${\mu _1} = 1.5$.
From the given figure,
The angle of incidence, $i = {60^ \circ }$.
The angle of refraction = ${90^ \circ }$.
According to Snell’s law of refraction the refractive index of liquid is:
$\dfrac{{\sin \,i}}{{\sin \,r}} = \dfrac{\mu }{{{\mu _1}}}$
Substitute the values of angle of incidence, angle of refraction, refractive index of the prism in the above equation;
$\dfrac{{\sqrt 3 }}{1} = \dfrac{\mu }{{1.5}} \\\ \mu = 1.3 \\\$
Therefore, the refractive index of the liquid on $AB$ is $\mu = 1.3$.
Hence, the option (C) $\mu = 1.3$ is the correct answer.

Note:- Snell’s law also referred to as the refractive law, is a formula used to outline the connection between the angles of incidence and angle of refraction, it represents to light passing along a boundary between two varying isotropic medium such as water, glass, or air.