Question
Question: Absorption of a gas follows Freundlich adsorption isotherm \(x\) is the mass of the gas adsorbed on ...
Absorption of a gas follows Freundlich adsorption isotherm x is the mass of the gas adsorbed on mass m of the adsorbent. The plot of logmx versus logp is shown in the given graph mx Is proportional to:
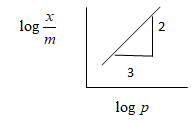
a.) P23
b.) P3
c.) P32
d.) P2
Solution
The relation between mx and P can be shown as mx=K.Pn1 ,apply natural log on both sides of the above equation and try to find out the slope of the graph obtained by the equation obtained after applying the log on both sides to find the answer for the above question.
Complete step by step solution:
We are having the relation between mx and P as mx=K.Pn1
Apply log on both sides, we obtain the following equation after applying the log
logmx=logK+n1logP
The graph of this equation is given as shown in the above diagram, where the slope of the graph of logmxversuslogP is n1 and the intercept is logK
From the above given graph we obtained the slope as n1=32
Put this slope in the above equation of the Freundlich adsorption isotherm
We obtain the final equation using the data given from the above graph is
mx=K.P32
This shows the relation between mx and P as mx is directly proportional to P32
So, the correct answer is “Option C”.
Note: From the relation mx=K.Pn1 it is a bit complicated to find the value of the power of P. We applied natural log on both sides so that we obtain a linear equation which represents the equation of a straight line. By plotting the graph of the equation we can simply calculate the slope which is nothing but the power of P and further putting the value of the slope in the original relation we obtained the required answer. This is one of the easier methods of finding unknowns of this type.
