Question

Abdul while driving to school computes the average speed for his trip to be 20Km/hr. On his return trip along the same route, there is less traffic and the average speed is 30Km/hr. What is the average speed for Abdul’s trip?

Answer 1

In order to solve these types of numerical problems it is important to first make sense of the path that is being followed by the person. This would help us compute properly the total distance covered and the total time taken to cover that distance.

Formula Used: The average speed of a body can be calculated using the expression:
${s_{av}} = \dfrac{d}{t}$ Where d is the total distance covered and t is the total time taken.

Complete step by step answer:
The path followed by Abdul can be represented using the figure given below:

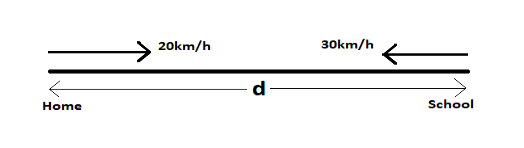
We begin by assuming the distance between Abdul’s home to his school to be d. Now we know that average velocity can only be calculated when the total distance is known. Thus, total distance covered by Abdul is given by:
$d + d = 2d$
In order to obtain the total time taken we have to find the time taken by Abdul to go from his home to his school and then return back from his school to his home.
Time taken by Abdul to go from his home to his school can be calculated by putting that value of total distance covered as ‘d’ and average speed as $20km{h^{ - 1}}$
Thus, $t = \dfrac{d}{{20}}$
Similarly, time taken by Abdul to return back to his home from his school can be calculated by putting the value total distance covered as ’d’ and average speed as $30km{h^{ - 1}}$.
Thus, $t = \dfrac{d}{{30}}$
Now the total time taken by Abdul $= \dfrac{d}{{20}} + \dfrac{d}{{30}} = \dfrac{{5d}}{{60}} = \dfrac{d}{{12}}$
Now in order to calculate the average speed we have to divide the total distance covered by Abdul by the total time taken by Abdul to cover the distance. Thus,
$\ {s_{av}} = \dfrac{{2d}}{{\dfrac{d}{{12}}}} \\\ \Rightarrow {s_{av}} = 2 \times 12 = 24 km{h^{ - 1}} \\\ \$
Hence, we find that the average speed of Abdul throughout the trip is $24km{h^{ - 1}}$.

Note: It is always important to first find total distance covered and total time taken individually and then proceed to find the value of the average speed. Average speed and instantaneous speed are two different concepts so do not get confused.