Question

Abdul while driving to school computes the average speed for his trip to be 20 $\text{km}{{\text{h}}^{-1}}$ . On his return trip along the same route, there is less traffic and the average speed is 40 $\text{km}{{\text{h}}^{-1}}$ . What is the average speed for Abdul’s trip?
A.) 26.6 $\text{km}{{\text{h}}^{-1}}$
B.) 30 $\text{km}{{\text{h}}^{-1}}$
C.) 13.3 $\text{km}{{\text{h}}^{-1}}$
D.) 60 $\text{km}{{\text{h}}^{-1}}$

Answer 1

Hint: To find the average speed we need to find the total distance and the total time taken. We will let the total distance be d and then we will find the time taken in each case from the velocity-time-distance relation. Then we can find the average speed.
Formula used:
$\text{Average speed = }\dfrac{\text{total distance covered}}{\text{total time taken}}$

Complete step by step answer:
Average speed can be defined as the ratio of total distance covered to the total time taken to cover the distance.

$\text{Average speed = }\dfrac{\text{total distance covered}}{\text{total time taken}}$

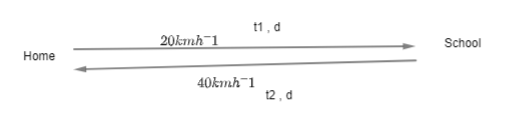
Let, the distance from home to school is d.
We need to find the total time.
Now, when going from home to school the average speed is 20 $\text{km}{{\text{h}}^{-1}}$. The distance is d.

Let the time taken when going from home to school is ${{t}_{1}}$.

$\begin{aligned} & \text{Speed = }\dfrac{\text{distance}}{\text{time}} \\\ & s=\dfrac{d}{{{t}_{1}}} \\\ & {{t}_{1}}=\dfrac{d}{s} \\\ & {{t}_{1}}=\dfrac{d}{20} \\\ \end{aligned}$

Now, when going from school to home the average speed is 40 $\text{km}{{\text{h}}^{-1}}$. The distance is d.

Let, the time taken is ${{t}_{2}}$

$\begin{aligned} & s=\dfrac{d}{{{t}_{2}}} \\\ & {{t}_{2}}=\dfrac{d}{s} \\\ & {{t}_{2}}=\dfrac{d}{40} \\\ \end{aligned}$

Now we can find the average speed.

$\begin{aligned} & \text{Average speed = }\dfrac{\text{total distance covered}}{\text{total time taken}} \\\ & \text{Average speed = }\dfrac{d+d}{{{t}_{1}}+{{t}_{2}}} \\\ & \text{Average speed = }\dfrac{2d}{\dfrac{d}{20}+\dfrac{d}{40}} \\\ & \text{Average speed = }\dfrac{2d}{\dfrac{2d+d}{40}} \\\ & \text{Average speed = }\dfrac{2d}{\dfrac{3d}{40}} \\\ & \text{Average speed = }\dfrac{2\times 40}{3} \\\ & \text{Average speed = 26}\text{.6 km}{{\text{h}}^{-1}} \\\ \end{aligned}$

The correct option is (A)

Note: Average speed and average velocity are different. Speed is a scalar quantity and the velocity is a vector quantity. For the above question if we are asked to find the average velocity, the answer will be zero. It is because the object returned to its starting point. So, its displacement will be zero and hence, the average velocity will be zero.