Question
Question: \(ABCP\) is a quadrant of a circle of radius 14\(cm\). With \(AC\) as a diameter, a semicircle is dr...
ABCP is a quadrant of a circle of radius 14cm. With AC as a diameter, a semicircle is drawn. Find the area of a shaded portion.
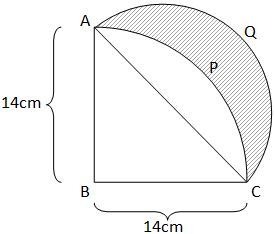
A. 47cm2 B. 72cm2 C. 98cm2 D. None of these
Solution
Hint: In this question, to find the area of shaded portion we have to calculate the area of region ACP by subtracting area quadrant of circle ABCP and area of triangle ΔABC.Then subtract it from the area of semicircle ACQ using area of circle =πr2 to get the required shaded area.
Complete step-by-step answer:
In right angle triangle ABC,
Using Pythagoras theorem
AB2+BC2=AC2 142+142=AC2 2×142=AC2 or, AC=2×142 AC=2×14=142cm
Area of region ACP= Area of quadrant ABCP- Area of ΔABC
=41×πr2−21×14×14 =41×722×14×14−7×14 =154−98 =56cm2
Now, area of shaded portion = Area of semicircle ACQ-Area of region ACP
=21×722×(2142)2−56 =21×722×72×72−56 =154−56 =98cm2
Therefore, the area of shaded region is 98cm2
Hence, the correct option is C.
Note: In order to solve such questions where the area under the shaded portion needs to be found out the basic step is to find out the geometrical figures around the shaded portion as sometimes the shaded portion might not be in some known geometrical form. So, we mostly find out the geometrical figures at the boundary of the region and subtract the area between them.
