Question
Question: ABCDEFGH is a cuboid. Find the angle between AG and plane EFGH(angle AGE). .
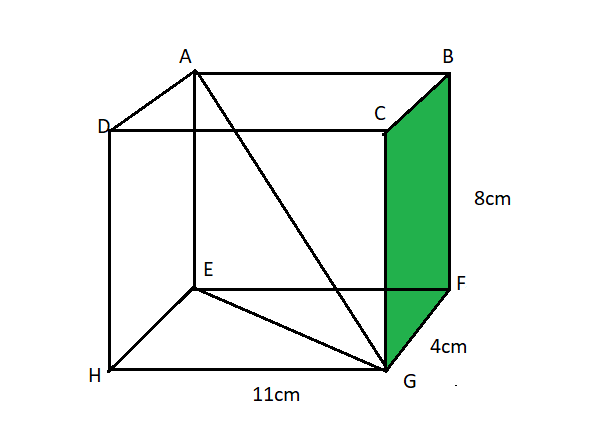
Solution
Hint: In this question first we need to find the unknowns involved in the ΔAEG which will be used to find the ∠AGE that is the angle between line AG and plane EFGH. Using Pythagoras theorem, we have to find the length of EG. And then apply the trigonometric ratios to find the required angle.
Complete step-by-step answer:
In ΔEFG
We have,
∠EFG=90∘
FG=4cm
EF=11cm
Now, apply Pythagoras theorem in ΔEFG
⇒(EG)2=(EF)2+(FG)2 ⇒(EG)2=112+42 ⇒(EG)2=137 ⇒EG=137 –eq.1
In ΔAEG
We have,
∠AEG=90∘
AE=8cm
And EG=137 {from eq.1}
Now, on applying trigonometric ratios in ΔAEG
⇒tan(∠AGE)=EGAE ⇒tan(∠AGE)=1378 ⇒tan(∠AGE)=0.6837
Now, using inverse trigonometric relations, we get
⇒∠AGE=tan−1(0.6837) ⇒∠AGE=34.36∘
Hence, the angle between AG and plane EFGH(∠AGE) is 34.36∘.
Note:- Whenever you get this type of question the key concept to solve is to learn the concept of Pythagoras theorem and how it is applied in a right angled triangle and trigonometric ratios. And one more thing to learn is the properties of inverse trigonometric relations.
