Question
Question: ABCDEF is a regular hexagon whose centre is O. Then \(\overline{AB}+\overline{AC}+\overline{AD}+\ove...
ABCDEF is a regular hexagon whose centre is O. Then AB+AC+AD+AE+AF is
(a) 2AO
(b) 3AO
(c) 5AO
(d) 6AO
Solution
Hint: First, we will construct the regular hexagon ABCDEF with center O. Then, we know from the study of the vectors we get AB+BC=AC. Then, by using the similar conditions of the vectors for the other sides, we get more relations. Then, we got to know that ABand AC are vectorially opposite to DE and DF.Then by using this condition, we get our final answer.
Complete step-by-step solution:
In this question, we are supposed to find the relational value of AB+AC+AD+AE+AFin a regular hexagon.
So, firstly we will construct the regular hexagon ABCDEF with center O as:
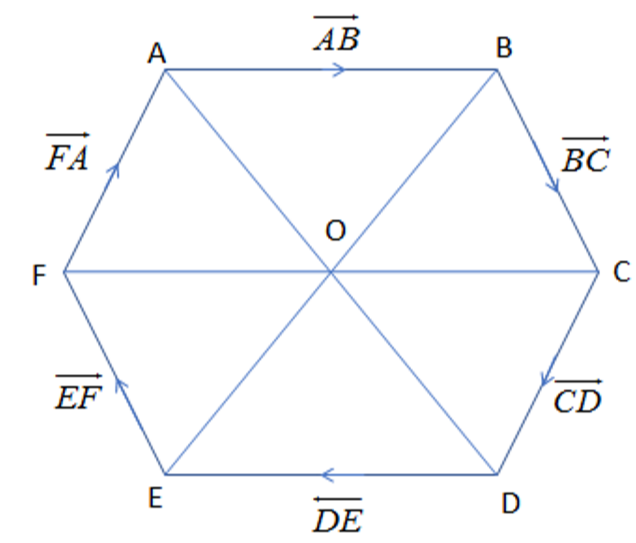
So, we know from the study of the vectors and the diagram as:
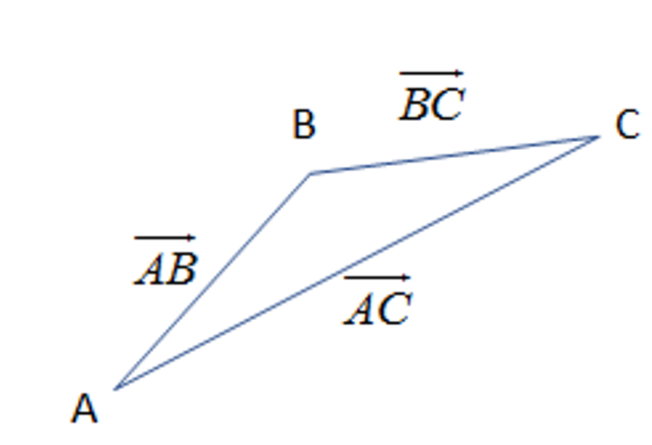
AB+BC=AC
So, by using the above relation, we get the following expression as:
