Question

ABCDEF is a regular hexagon whose center is O. The $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AF}$ is
(a)$2\overrightarrow{AO}$
(b)$3\overrightarrow{AO}$
(c)$5\overrightarrow{AO}$
(d)$6\overrightarrow{AO}$

Answer 1

Hint: In the figure below we have a regular hexagon $ABCDEF$ . In this question we can use the concept of addition of vectors using parallelogram law of addition.

Complete step by step answer:

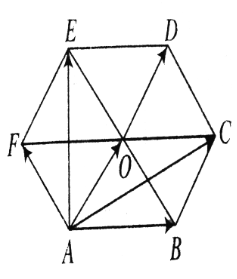
We can regroup these vectors into pairs and then add each pair individually such that we can write the result in terms of $\overrightarrow{AO}$ .

We can rewrite the sum $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AF}$ by regrouping the terms as given below:
$(\overrightarrow{AB}+\overrightarrow{AF})+(\overrightarrow{AC}+\overrightarrow{AE})+\overrightarrow{AD}$
First we evaluate the sum $\overrightarrow{AB}+\overrightarrow{AF}$ . To evaluate it we first observe that $ABOF$ is parallelogram (more precisely, it is a rhombus). Thus, we can easily see that the resultant vector is $\overrightarrow{AO}$ .
Now we evaluate the sum $\overrightarrow{AC}+\overrightarrow{AE}$ . Since, $ABCDEF$ is regular hexagon we can prove $OA=OB=OC=OD=OE=OF$ and hence $ABCO$ and $AFEO$ are rhombus. This implies that diagonals $AC$ and $AE$ bisect angles $OAF$ and $OAB$ respectively. Therefore,
$\angle EAD=\angle CAD=\dfrac{\pi }{6}$
Thus, $\angle EAC=\dfrac{\pi }{3}$
By symmetry we can also prove that $\angle AED=\angle ACD=\dfrac{\pi }{6}$ . Therefore, $AE=AC=AD\cos \dfrac{\pi }{6}=\sqrt{3}.AO$ (since, $\overrightarrow{AD}=2.\overrightarrow{AO}$ ).
Since $AD$ is the bisector of $\angle EAC$ we can see that the resultant of $\overrightarrow{AE}+\overrightarrow{AC}$ lies along $\overline{AO}$ i.e. $\widehat{AO}$ . We can calculate the magnitude of the resultant by using the following formula

& |\overrightarrow{AE}+\overrightarrow{AC}|\ =\sqrt{|\overrightarrow{AC}{{|}^{2}}+|\overrightarrow{AE}{{|}^{2}}+2.|\overrightarrow{AC}||\overrightarrow{AE}|\cos \dfrac{\pi }{3}} \\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{3.|\overrightarrow{AO}{{|}^{2}}+3.|\overrightarrow{AO}{{|}^{2}}+2.3.|\overrightarrow{AO}||\overrightarrow{AO}|.\dfrac{1}{2}} \\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{9.|\overrightarrow{AO}{{|}^{2}}} \\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =3.|\overrightarrow{AO}| \\\ \end{aligned}$$ Therefore, $$|\overrightarrow{AE}+\overrightarrow{AC}|=3.|\overrightarrow{AO}|.\widehat{AO}=3.|\overrightarrow{AO}|$$ So finally we have, $$\begin{aligned} & (\overrightarrow{AB}+\overrightarrow{AF})+(\overrightarrow{AC}+\overrightarrow{AE})+\overrightarrow{AD} \\\ & =\overrightarrow{AO}+3.\overrightarrow{AO}+2.\overrightarrow{AO} \\\ & =6.\overrightarrow{AO} \\\ \end{aligned}$$ Hence, the correct answer is (d). Note: Major part of this problem could be solved without much calculation and just by using the symmetry of the geometrical shape given. Once we identified the correct pair of vectors to sum up individually, the rest of the work was trivial. While solving problems based on addition of vectors, one should try to simplify the problem as much as possible if symmetry in the given problem allows so. However, there are several places where one can easily commit mistakes especially in the part where we had to calculate$\overrightarrow{AC}+\overrightarrow{AE}$ . It is important that we solve the question using very basic principles of vectors and not overcomplicate the problem.