Solveeit Logo
Login

Question

Question: ABCDE is a regular pentagon of uniform wire. The rate of heat entering at A and leaving at C is equa...

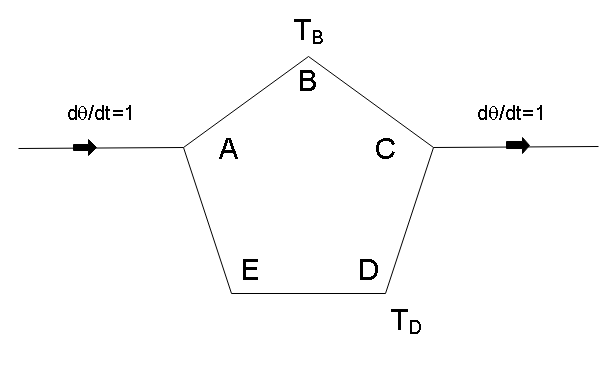
ABCDE is a regular pentagon of uniform wire. The rate of heat entering at A and leaving at C is equal TB{T_B} ​and TD{T_D} ​are the temperature of B and D. Find the temperature TC{T_C}​:

A)3TB+2TD5\dfrac{{3{T_B} + 2{T_D}}}{5}
B)3TD−2TB3{T_D} - 2{T_B}
C)2TD−2TB2{T_D} - 2{T_B}
D) Can have any value

Explanation

Solution

The heat flow in the pentagon will behave similarly to the current flow in wires with a similar configuration. The heat flow will split into the two branches similar to the splitting of current in parallel resistors.

Complete step by step answer:
We’ve been given that ABCDE is a regular pentagon. Let us denote the heat conductivity of each wire with KK. Then the net conductivity for the flow of heat from the branch ABC (branch-1) will be 2K2K since wires are in series.
Similarly, the conductivity in the branch AEDC (branch-2) will be 3K3K.
Hence the heat flow in the two branches will be in the inverse ratio of the conductivity of the two branches which will be
Q1Q2=3K2K=32\dfrac{{{Q_1}}}{{{Q_2}}} = \dfrac{{3K}}{{2K}} = \dfrac{3}{2}
Let us consider the wires BC and DC. In both the wires, the heat flow will depend on the temperature at point C. For wire BC, the heat flow will be proportional to
Q1∝(TC−TB){Q_1} \propto ({T_C} - {T_B})
And the heat flow in the DC wire will be
Q2∝(TC−TD){Q_2} \propto ({T_C} - {T_D})
Then taking the ratio of the two above equations, we get
Q1Q2=TC−TBTC−TD\dfrac{{{Q_1}}}{{{Q_2}}} = \dfrac{{{T_C} - {T_B}}}{{{T_C} - {T_D}}}
Since we know Q1Q2=32\dfrac{{{Q_1}}}{{{Q_2}}} = \dfrac{3}{2}, we can write
32=TC−TBTC−TD\dfrac{3}{2} = \dfrac{{{T_C} - {T_B}}}{{{T_C} - {T_D}}}
Cross multiplying the denominators, it can be simplified to
3TC−3TD=2TC−2TB3{T_C} - 3{T_D} = 2{T_C} - 2{T_B}
Which gives us
TC=3TD−2TB{T_C} = 3{T_D} - 2{T_B}
Hence, the correct choice is option (B).

Note: We should know that heat flow in a series of wires is constant. However, the neat heat flow will split into the inverse of the conductivity of the cables when two branches are connected in parallel. We don’t need to know the numerical value of all the temperatures at all the different wires but only need to use the laws of heat conduction.