Question

ABCD is a trapezium such that AB and CD are parallel and BC ⊥ CD. If ∠ADB=θ, BC=p and CD =q, then AB is equal to
A. $\dfrac{{{p^2} + {q^2}\cos \theta }}{{p\cos \theta + q\sin \theta }}$
B. $\dfrac{{{p^2} + {q^2}}}{{{p^2}\cos \theta + {q^2}\sin \theta }}$
C. $\dfrac{{\left( {{p^2} + {q^2}} \right)\sin \theta }}{{{{\left( {p\cos \theta + q\sin \theta } \right)}^2}}}$
D. $\dfrac{{\left( {{p^2} + {q^2}} \right)\sin \theta }}{{\left( {p\cos \theta + q\sin \theta } \right)}}$

Answer 1

In order to solve this question we need to draw the diagram and then apply the formula of trigonometry using cos and sin that is we need to know must the formula of $\cos \alpha = \dfrac{q}{{\sqrt {{p^2} + {q^2}} }} and \sin \alpha = \dfrac{p}{{\sqrt {{p^2} + {q^2}} }}$. Then we have to use sine formula to get the value of AB and then on solving we will get the right answer.

Complete step-by-step answer :

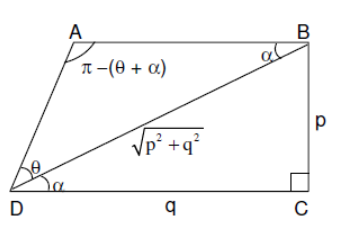
In the triangle BCD $\cos \alpha = \dfrac{q}{{\sqrt {{p^2} + {q^2}} }}and\sin \alpha = \dfrac{p}{{\sqrt {{p^2} + {q^2}} }}$
Using sine rule in triangle ABD we get the equation as,
$\dfrac{{AB}}{{\sin \theta }} = \dfrac{{BD}}{{\sin \left( {\theta + \alpha } \right)}}$
Then we get the value of AB as,
$\Rightarrow AB = \dfrac{{\sqrt {{p^2} + {q^2}} \sin \theta }}{{\sin \theta \cos \alpha + \cos \theta \sin \alpha }}$
Then on putting the values obtained above of cos and sin we get the new equation as,
$\Rightarrow \dfrac{{\sqrt {{p^2} + {q^2}} \sin \theta }}{{\dfrac{{\sin \theta q}}{{\sqrt {{p^2} + {q^2}} }} + \dfrac{{\cos \theta p}}{{\sqrt {{p^2} + {q^2}} }}}}$
After solving it further we get the value of AB as:
$\Rightarrow AB = \dfrac{{\left( {{p^2} + {q^2}} \right)\sin \theta }}{{\left( {p\cos \theta + q\sin \theta } \right)}}$

Note : A trapezium is a quadrilateral with two parallel sides. The parallel sides of a trapezium are called bases and the non-parallel sides of a trapezium are called legs. It is also called a trapezoid. Sometimes the parallelogram is also called a trapezoid with two parallel sides.