Question

$ABCD$ is a square of side $4{\text{ cm}}$.If E is a point in the interior of the square such that $\Delta CED$ is equilateral, then find the area of $\Delta ACE$ (in $c{m^2}$). $$$$

Answer 1

The area of a square $ABCD$ is $a \times a = {a^2}$
Diagonal of the square is $\sqrt {{a^2} + {a^2}} = \sqrt {2{a^2}} = \sqrt 2 a$

Let, $\Delta ABC$ be an equilateral triangle then the sides of the triangle are equal.
Suppose the sides of the triangle is a unit, then the area of the triangle is $\dfrac{{\sqrt 3 }}{4}{a^2}$
The height of the triangle is $\dfrac{{\sqrt 3 }}{2}a$
With help of the above formula we will find the area of $\Delta ACE$.

Complete step by step answer:
It is given that, $ABCD$ is a square of side $4cm$.
Also, $E$ is a point in the interior of the square such that $\Delta CED$ is equilateral,
Let $ABCD$ be a square of side $4cm$

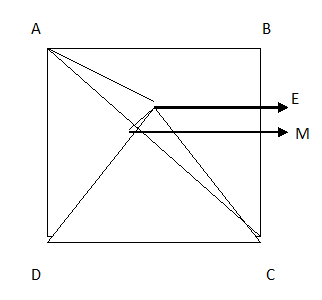
That is $AB = BC = CD = DA = 4{\text{ }}cm$
Also given that $\Delta CED$ is an equilateral triangle.
$EC = CD = DE = 4{\text{ }}cm$
$\angle ECD = {60^ \circ }$ since it is the angle of an equilateral triangle
Let $AC$ be a diagonal of the square $ABCD$.
Therefore, $\angle ACD{\text{ }} = {\text{ }}45^\circ$
We know that $\angle ECA{\text{ }} = \angle ECD{\text{ }} - \angle ACD{\text{ }}\;$
By substituting the values of the angles we know we get,
$\angle ECA{\text{ }} = 60^\circ {\text{ }} - {\text{ }}45^\circ = 15^\circ$
In $\Delta ACE$, let us draw a perpendicular $EM$ the base $AC$.
Now in $\Delta EMC$, using the following formula we will find the value of $EM$.
$\sin 15^\circ = \dfrac{{EM}}{{EC}}$
Let us substitute the value of $EC$, we get,
$\sin 15^\circ = \dfrac{{EM}}{4}$
Let us substitute the value of the trigonometric function we get,
$\dfrac{{EM}}{4} = \dfrac{{\sqrt 3 - 1}}{{2\sqrt 2 }}$
Let us rationalize the denominator therefore we get,
$\dfrac{{EM}}{4} = \dfrac{{(\sqrt 3 - 1) \times \sqrt 2 }}{{2\sqrt 2 \times \sqrt 2 }}$
$\dfrac{{EM}}{4} = \dfrac{{\sqrt 2 (\sqrt 3 - 1)}}{4}$
Let cancel out the same terms in the above equation we get,
$EM = \sqrt 2 (\sqrt 3 - 1)cm$
The Diagonal of a square is $AC$ its value is given by $\sqrt 2 a$
Since $a = 4cm$ by substituting the value of a in the above equation we get,
$\sqrt 2 a = \sqrt 2 \times 4 = 4\sqrt 2 cm$
Hence $AC = 4\sqrt 2 cm$
Now let us find the area of $\Delta AEC$,
We know the area of triangle is given by the formula $A = \dfrac{1}{2} \times {\text{height X base}}$
In $\Delta AEC$, height is $EM$ and base is $AC$.
Therefore we get,
$A = \dfrac{1}{2} \times EM \times AC$
Let us substitute the values we know we get,
$A = \dfrac{1}{2} \times \sqrt 2 (\sqrt 3 - 1) \times 4\sqrt 2$
On solving the values in the above equation we get,
$A = \dfrac{1}{2} \times 8(\sqrt 3 - 1) = 4(\sqrt 3 - 1)c{m^2}$
We have found the Area of $\Delta AEC$ is $4(\sqrt 3 - 1)c{m^2}$
Hence, the area of $\Delta AEC$ is $4(\sqrt 3 - 1)c{m^2}$.

Note:
We have used the value of the ${\text{sin }}15^\circ$.
Let us calculate the value using the formula,
$\sin (A - B) = \sin A\cos B - \cos A\sin B$
Now,
$\sin 15^\circ = \sin (45^\circ - 30^\circ )$
$= \sin 45^\circ \cos 30^\circ - \cos 45^\circ \sin 30^\circ$
$= \dfrac{1}{{\sqrt 2 }} \times \dfrac{{\sqrt 3 }}{2} - \dfrac{1}{{\sqrt 2 }} \times \dfrac{1}{2}$
$= \dfrac{{\sqrt 3 - 1}}{{2\sqrt 2 }}$